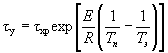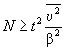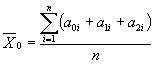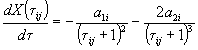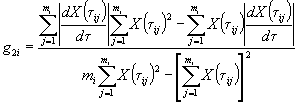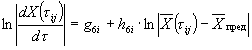ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ЕДИНАЯ СИСТЕМА ЗАЩИТЫ
ОТ КОРРОЗИИ И СТАРЕНИЯ
МАТЕРИАЛЫ ПОЛИМЕРНЫЕ
МЕТОДЫ УСКОРЕННЫХ ИСПЫТАНИЙ
НА КЛИМАТИЧЕСКОЕ СТАРЕНИЕ
ГОСТ 9.707-81
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
Москва
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
|
Единая система защиты от коррозии и старения МАТЕРИАЛЫ ПОЛИМЕРНЫЕ Методы ускоренных испытаний
на Unified system of corrosion and ageing |
ГОСТ |
Срок действия с 01.01.83
до 01.07.95
Настоящий стандарт распространяется на полимерные материалы, детали и узлы из них в ненапряженном состоянии, а также на резиновые детали в напряженном состоянии (сжатие радиальное до 25 %, осевое до 45 %) и устанавливает методы ускоренных испытаний для определения и прогнозирования изменения свойств при термовлажностном климатическом старении в условиях хранения 1, 2, 3, 4, 5 (в упаковке и без нее) и эксплуатации категории 2, 3, 4, 5 по ГОСТ 15150-69.
Определение и прогнозирование изменения свойств проводят по одному или нескольким характерным показателям старения. Показатель устанавливают в стандартах или технических условиях на материал, узел или деталь.
Факторами климатического старения в настоящем стандарте являются: температура (положительная, отрицательная, сезонные и суточные циклические ее изменения) и влажность воздуха.
Статистические характеристики климатических факторов, необходимые для установления режимов испытаний, имитирующих условия хранения под навесом, устанавливают по ГОСТ 16350-80 и ГОСТ 24482-80.
Характеристики температуры и влажности, необходимые для установления режимов испытаний, имитирующих условия хранения в отапливаемых и неотапливаемых хранилищах, устанавливают по данным распределения температуры в них, статистически обработанным за период наблюдения не менее пятнадцати лет. При отсутствии данных о распределении температуры в неотапливаемых хранилищах характеристики температуры в них устанавливают по ГОСТ 16350-80.
Методы настоящего стандарта применяют для исследовательских испытаний. Результаты испытаний по согласованию с заказчиком включают в стандарты или технические условия на материал, деталь или узел и используют для определения и прогнозирования сохраняемости изделий при воздействии указанных факторов.
Термины, применяемые в стандарте, и пояснения к ним приведены в приложении 1.
1. МЕТОД 1
Для узлов прогнозирование изменения свойств проводят по изменению показателя слабого звена.
1.2. Испытания материалов деталей и узлов, хранение которых осуществляется в герметичных условиях
1.2.1.1. Материалы перед испытаниями подвергают той же технологической обработке (воздействию температуры, давления), что и при изготовлении изделий.
1.2.1.2. Форма и размеры образцов для испытаний, способ и режимы их изготовления должны соответствовать требованиям, установленным в стандартах на метод определения показателя.
1.2.1.3. Испытания материалов проводят на заготовках, размер которых позволяет изготовить после испытаний не менее двух образцов.
Пример изготовления заготовок и группировки их на каждый съем приведен в приложении 2.
1.2.1.4. Образцы для определения показателя до и после испытаний должны быть изготовлены из одной партии материала.
1.2.1.5. Продолжительность и условия хранения образцов от изготовления до испытаний должны быть указаны в стандартах или технических условиях на материал, деталь, узел. При отсутствии таких указаний продолжительность хранения образцов от изготовления до испытаний не должна превышать 28 сут при нормальных значениях климатических факторов по ГОСТ 15150-69.
Образцы материалов, узлов, деталей, предназначенных для хранения в герметичных условиях, до испытаний хранят в герметичных контейнерах при температуре (293±5) К (20±5) °С.
1.2.1.6. Количество образцов (N) для определения исходного значения показателя и на каждый из съемов вычисляют в соответствии с приложением 3.
Испытательная камера и термостат, обеспечивающие поддержание температуры с предельной допускаемой погрешностью ±2 К до 522 К (±2 °С до 249 °С) и ±3 К от 523 К и выше (±3 °С от 250 °С и выше). Испытательная камера должна обеспечивать регулирование и поддержание относительной влажности воздуха с предельной допускаемой погрешностью ±3 % и предельно допускаемый перепад температуры в рабочем объеме ±2 К (±2 °С).
Контейнер, снабженный крышкой с прокладкой, обеспечивающей его герметичность, и устройством для размещения образцов.
Испытательная камера, термостат и контейнер должны быть изготовлены из материалов, не оказывающих влияния на результат испытаний, и должны обеспечивать проведение испытаний заданного количества образцов.
Термоэлектрический преобразователь.
Весы с предельной допускаемой погрешностью ±0,01 %.
(Измененная редакция, Изм. № 1).
1.2.3. Подготовка к испытаниям
1.2.3.1. Для проведения испытаний составляют программу, в которой указывают:
объект испытаний (марку материала, детали, узла), завод-изготовитель, способ изготовления;
цель испытаний;
предполагаемые условия хранения;
характерный показатель старения и его предельно допускаемое значение;
режим испытаний и периодичность съемов;
перечень используемых при испытаниях стандартов или технических условий;
метрологическое обеспечение испытаний;
обозначение настоящего стандарта.
1.2.4. Проведение испытаний
1.2.4.3. Свободный объем контейнера заполняют металлическим вкладышем с ячейками по форме и размерам образцов или шариками из стекла диаметром не более 15 мм. Материал вкладыша не должен оказывать влияния на результат испытаний.
1.2.4.4. Контейнеры с образцами помещают в термостаты. Расстояние между стенками термостата и контейнера должно быть не менее 50 мм, между контейнерами - не менее 20 мм.
(Измененная редакция, Изм. № 1).
1.2.4.5. Термическое старение проводят при температурах Т1 < Т2 < Т3 < ... < Тn, где n ³ 4. Интервал между температурами испытаний должен быть не менее 10 К (10 °С).
1.2.4.6. Минимальная температура испытаний Т1 должна быть равна или выше абсолютного максимума температуры хранения материала.
1.2.4.7. Максимальная температура испытаний Тmах должна быть на 10 К (10 °С) ниже температуры, при которой в материале образца начинаются физические и (или) химические процессы, не имеющие место при температуре хранения (или эксплуатации).
1.2.4.8. Температура испытаний Тп должна быть равна или меньше Тmах.
1.2.4.9. Максимальную температуру испытаний Тmах определяют по ГОСТ 9.715-86.
1.2.4.7 - 1.2.4.9. (Измененная редакция, Изм. № 1).
1.2.4.10. Продолжительность испытаний при каждой температуре не должна быть меньше, чем требуется для получения существенных изменений показателя. Существенность изменения показателя устанавливают в соответствии с приложением 4.
1.2.4.11. Испытания узлов проводят по каждому из составляющих его материалов.
1.2.4.12. Предварительно, с помощью термоэлектрического преобразователя, устанавливают продолжительность прогрева, необходимую для достижения по всему объему образца температуры, отличающейся от заданной по п. 1.2.4.5 на ±1 К (±1 °С). Отсчет продолжительности испытаний начинают после указанного прогрева.
(Измененная редакция, Изм. № 1).
1.2.4.13. Испытания проводят непрерывно в течение всей продолжительности старения. В продолжительность старения не входит продолжительность вынужденных перерывов, которая не должна превышать 10 сут. При вынужденных перерывах образцы хранят в соответствии с требованиями п. 1.2.1.5.
1.2.4.14. Если испытания проводят для определения продолжительности хранения до достижения заданного значения показателя, то испытания ограничивают продолжительностью старения до достижения указанного значения показателя.
1.2.4.15. Если испытания при температуре Т ³ 353 К (80 °С) в течение 30 сут или при Тn = 333 К (60 °С) в течение 90 сут не привели к существенным изменениям показателя, то проводят дополнительные испытания при температуре Тп, продолжительность старения при этом вычисляют по формуле
где tу, Тп - соответственно продолжительность и температура испытаний, ч, К;
tхр - заданная продолжительность хранения, ч;
E = 41,868×103 Дж/моль (10 ккал/моль);
Тэ - эквивалентная температура, установленная для заданного значения Е по приложению 5, К;
R = 8,314 Дж/моль×К (1,987 кал/моль×°С).
Если при этом не будет получено существенное изменение показателя, испытания прекращают; материал считают стойким к воздействию указанных климатических факторов по заданному показателю.
1.2.4.16. В процессе старения при каждой температуре, указанной в п. 1.2.4.5, периодически, не менее 10 раз, проводят съемы образцов для определения показателя.
1.2.4.15; 1.2.4.16. (Измененная редакция, Изм. № 1).
1.2.4.17. При каждом из съемов отбирают по 1 контейнеру и охлаждают его до температуры (293±5) К (20±5) °С. Продолжительность хранения образцов в контейнере после охлаждения должна быть не более 10 сут. Затем образцы извлекают из контейнера и проводят определение показателя в соответствии со стандартами на метод его определения.
1.2.4.18. Результаты испытаний записывают в протокол по форме, приведенной в приложении 4.
1.2.5.1. Значение показателя в исходном состоянии и после каждого съема принимают равным среднему арифметическому значению показателя, которое вычисляют в соответствии с требованиями ГОСТ 269-66.
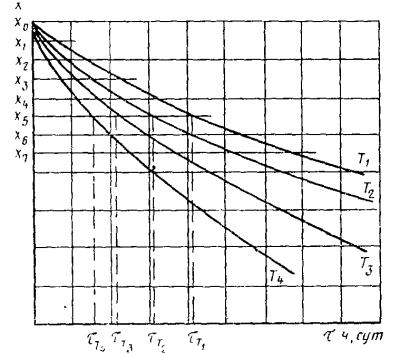
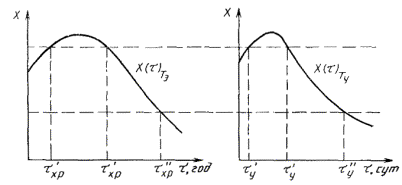
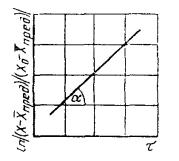
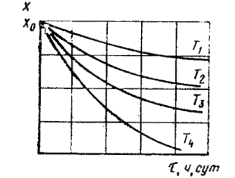
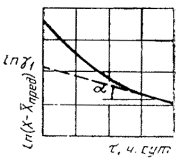
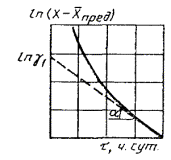
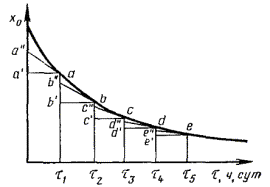
1.2.5.2. Данные, полученные по п. 1.2.5.1, в случае монотонного изменения показателя в процессе старения, обрабатывают методом наименьших квадратов, применяя обратный полином второй степени в соответствии с рекомендуемым приложением 6, и строят график зависимости изменения показателя от продолжительности старения при температурах t1, Т2, Т3, ..., Тп, как показано на черт. 1.
1.2.5.3. На оси ординат графика, представленного на черт. 1, откладывают различные значения показателя X1, Х2, ..., Хm при т ³ 5, проводят прямые, параллельные оси абсцисс, до пересечения с кривыми графика, как показано на черт. 1 и определяют продолжительность испытаний (ti) до достижения заданных значений показателя (X1, Х2, ..., Хm) при температурах (t1, Т2, Т3, ..., Тп) или вычисляют ti в соответствии с приложением 6.
Черт. 1
1.2.5.4. Для каждого значения показателя Xi вычисляют коэффициенты ei, кДж/моль (ккал/моль), для каждой пары температур Т1 и Т2, Т2 и T3, Тп-1 и Тn по формуле
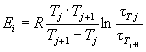 ,
,
где Tj, Tj+1 - температуры испытаний, К;
j = 1, 2, ..., (n - 1);
![]() ,
, ![]() - соответственно
продолжительность испытаний до достижения каждого значения показателя Xi при
температурах tj и tj+1.
- соответственно
продолжительность испытаний до достижения каждого значения показателя Xi при
температурах tj и tj+1.
Если вычисленные коэффициенты Ei изменяются монотонно, то допускаемое различие между максимальным и минимальным значениями Ei для каждого значения показателя должно быть не более 25,1 кДж/моль (6,0 ккал/моль); при немонотонном изменении Ei - 41,868 кДж/моль (10,0 ккал/моль).
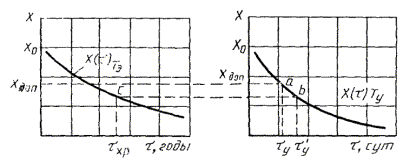
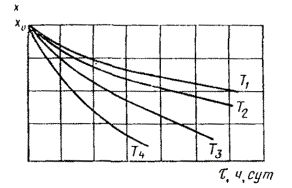
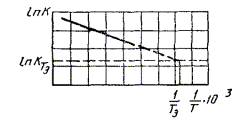
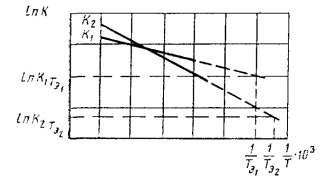
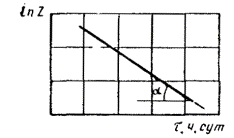
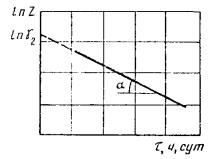
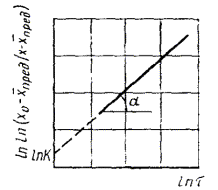
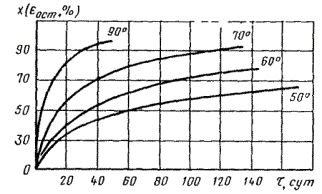
1.2.5.5. Данные о зависимости продолжительности испытаний до достижения каждого значения показателя X1, X2, Х3, ..., Xm при каждой температуре T1, T2, T3, ..., Tn, полученные по п. 1.2.5.3, обрабатывают методом наименьших квадратов, описывают уравнением прямой и строят график, как показано на черт. 2.
Черт. 2
Вычисляют тангенс угла наклона tgai каждой прямой к оси абсцисс по формуле
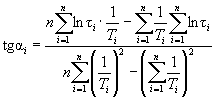 ,
,
где п - число температур испытаний.
1.2.5.6. Вычисляют коэффициент ej для каждого значения показателя Xi по формуле
![]() .
.
1.2.5.7. Вычисляют среднее арифметическое значение коэффициента Eср по формуле
![]() ,
,
где т - число значений показателя.
Если вычисленное значение Еср ³ 63 кДж/моль (15 ккал/моль), то допускаемое отклонение Еj между различными значениями показателя в случае монотонного его изменения не должно превышать ±5,3 кДж/моль (±1,25 ккал/моль); в случае немонотонного изменения - ±10,5 кДж/моль (±2,5 ккал/моль).
Если вычисленное значение Еср ³ 63 кДж/моль (15 ккал/моль), то допускаемые отклонения не должны превышать соответственно ±10,5 кДж/моль (±2,5 ккал/моль) и ±21 кДж/моль (±5,0 ккал/моль).
1.2.5.8.
По значению Ecp,
вычисленному по п. 1.2.5.7, и значению Тэ,
установленному в соответствии с обязательным приложением 5,
вычисляют продолжительность испытаний ![]() до достижения
значений X1, X2, Х3,
..., Xm
при Тэ по формуле
до достижения
значений X1, X2, Х3,
..., Xm
при Тэ по формуле
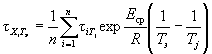 ,
,
где i = l, 2, 3, ..., m; j = 1, 2, 3 ,..., n.
Если не указан конкретный климатический район предполагаемого хранения материала, узла, детали, то Тэ устанавливают для климатического района с очень жарким сухим климатом. Если указаны конкретные условия хранения, то Тэ устанавливают для заданных условий.
1.2.5.9. Относительное изменение показателя ai вычисляют по формуле
![]() ,
,
где X0 - исходное значение показателя, определенное по п. 1.2.4.1;
Xi - значение показателя, выбранное по п. 1.2.5.3.
(Измененная редакция, Изм. № 1).
1.2.5.10. (Исключен, Изм. № 1).
1.2.5.11.
Для учета погрешности прогноза вычисленные значения ![]() делят на коэффициент
1,5.
делят на коэффициент
1,5.
Строят график зависимости ai от ![]() (кривую прогноза).
(кривую прогноза).
(Измененная редакция, Изм. № 1).
1.2.5.12. По полученной кривой прогноза определяют значение показателя после заданной продолжительности хранения или продолжительность хранения до достижения заданного значения показателя.
1.2.5.13.
Если при выбранном значении показателя Хт прогнозируемая
продолжительность хранения ![]() меньше
заданной, то необходимо
вновь провести испытания, чтобы получить более значительные изменения
показателя.
меньше
заданной, то необходимо
вновь провести испытания, чтобы получить более значительные изменения
показателя.
Испытания повторяют лишь при тех значениях температуры, при которых кривые графика, приведенные на черт. 1, не позволяют определить продолжительность старения до достижения значений показателя Хm+1, Хm+2.
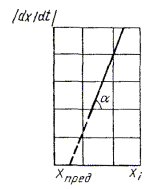
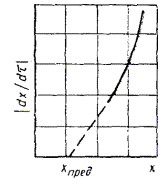
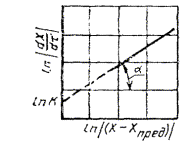
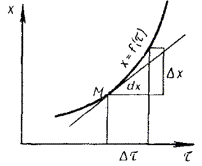
1.2.5.14. При невыполнении условий пп. 1.2.5.4 и 1.2.5.7 данные по изменению показателя от продолжительности старения при различных температурах обрабатывают аналитическими методами в соответствии с рекомендуемым приложением 7, используя способ графического дифференцирования, приведенный в приложении 8.
Пример обработки результатов испытаний приведен в приложении 9.
(Измененная редакция, Изм. № 1).
1.3. Испытания материалов, узлов и деталей, хранение которых осуществляют в негерметичных условиях
1.3.1. Отбор образцов
1.3.1.1. Образцы для испытаний должны соответствовать требованиям п. 1.2.1.
1.3.2. Аппаратура должна соответствовать требованиям п. 1.2.2.
1.3.2.1. Термостат должен обеспечивать полный обмен воздуха не менее трех и не более десяти раз в час. Термостат должен быть снабжен приборами для измерения и регулирования скорости воздухообмена.
1.3.3. Подготовка к испытаниям
1.3.3.1. Составляют программу испытаний в соответствии с требованиями, изложенными в п. 1.2.3.1.
Допускается проводить кондиционирование, выдерживая образцы в камере, в которой заданную влажность воздуха при заданной температуре устанавливают, применяя растворы солей.
Метод создания влажности воздуха над растворами солей приведен в приложении 10.
(Измененная редакция, Изм. № 1).
Допускается проводить кондиционирование до достижения образцами постоянного значения показателя, путем периодического его определения в соответствии со стандартами на метод определения показателя.
1.3.4. Проведение испытаний
1.3.4.1. После кондиционирования образцов по п. 1.3.3.2 определяют исходное значение показателя в соответствии со стандартом на метод его определения.
1.3.4.2. Устанавливают два режима испытаний. В режиме 1 испытания проводят при повышенных температурах T1 < T2 < ... < Tn, где n ³ 4 и постоянном значении абсолютной влажности воздуха (13,6±2,6) г/м3.
В режиме 2 испытания проводят при температуре (296±2) К (23 ±2) °С и следующих значениях абсолютной влажности воздуха q1 = (6,3±1,3) г/м3, q2 = (10,4±l,8) г/м3, q3 = (19,6±2,5) г/м3. Указанным значениям q1, q2, q3 при (296±2) К (23±2) °С соответствуют следующие значения относительной влажности воздуха: j1 = (30±3) %; j2 = (50±3) %; j3 = (96±3) %.
Допускается проводить испытания в режиме 1 при повышенных температурах T1 < T2 < ... < Tn и постоянном значении относительной влажности воздуха j1, j2 или j3, если при этом в материале образца не происходят необратимые физические процессы, которые не имеют место при хранении. Наличие необратимых процессов вследствие влагопоглощения материала при заданной температуре устанавливают соответствующими физическими методами (например, по изотермам сорбции).
(Измененная редакция, Изм. № 1).
1.3.4.3. Температуры испытаний Т1, Т2, ..., Тп устанавливают в соответствии с требованиями пп. 1.2.4.5 - 1.2.4.9.
1.3.4.4. Для испытаний в режиме 1 образцы помещают в термостаты с установленными в них температурой и влажностью в соответствии с требованиями п. 1.3.4.2. Заданное значение абсолютной влажности воздуха при испытаниях создают и поддерживают с помощью кондиционера, обеспечивающего в помещении, где проводят испытания, температуру (296±2) К (23±2) °С и относительную влажность воздуха (65±5) %.
(Измененная редакция, Изм. № 1).
Отсчет продолжительности испытаний устанавливают в соответствии с требованиями п. 1.2.4.12. Количество съемов образцов, устанавливают в соответствии с требованиями п. 1.2.4.16.
1.3.4.5. Перед испытаниями в режиме 2 определяют массу каждого из образцов взвешиванием с предельной допускаемой погрешностью ±0,01 %. Затем образцы помещают в испытательные камеры с установленными в них температурой и влажностью в соответствии с требованиями п. 1.3.4.2.
Допускается проводить испытания в камерах, в которых заданные значения влажности воздуха при заданной температуре устанавливают в соответствии с требованиями рекомендуемого приложения 10.
Периодически, через каждые 72 ч, образцы вынимают из камеры, взвешивают и определяют массу каждого из образцов с предельной допускаемой погрешностью ±0,01 %.
Продолжительность испытаний при каждом значении q устанавливают аналогично продолжительности кондиционирования образцов до достижения в них постоянной массовой доли влаги, в соответствии с требованиями п. 1.3.3.3.
(Измененная редакция, Изм. № 1).
1.3.5. Обработка результатов
1.3.5.1. Результаты испытаний в режиме 1 обрабатывают и строят кривую прогноза в соответствии с требованиями п. 1.2.5.
1.3.5.2. Для образцов, испытанных в режиме 2, при каждом значении влажности вычисляют коэффициент ri, учитывающий физическое влияние влажности воздуха на изменение показателя, по формуле
![]() ,
,
где Xqi - среднее арифметическое значение показателя при каждом из выбранных значений влажности qi, определенное по п. 1.3.4.7;
X0 - исходное значение показателя, определенное по п. 1.3.4.1.
Если r = 1 при всех значениях qi, то испытания образцов по п. 1.3 проводят без предварительного кондиционирования, установленного в п. 1.3.3.2.
Зависимость ri от qi описывают обратным полиномом второй степени в соответствии с рекомендуемым приложением 6, заменяя параметр ti на qi, учитывая, что при q = (13,6±2,6) г/м3 r = 1.
По полученному уравнению вычисляют коэффициент rхр для заданных условий хранения при qхр.
(Измененная редакция, Изм. № 1).
1.3.5.4. Кривую прогноза, построенную по п. 1.3.5.1, корректируют для учета влияния влажности воздуха в заданных условиях хранения. Корректировку осуществляют путем умножения ординат кривой прогноза на коэффициент rхр, вычисленный по п. 1.3.5.3.
1.3.5.5. По кривой прогноза, построенной по п. 1.3.5.4, определяют значение показателя после заданной продолжительности хранения в заданных условиях или продолжительность хранения до достижения заданного значения показателя.
2. МЕТОД 2
2.1.1. Виды и последовательность воздействия указанных климатических факторов в цикле устанавливают в зависимости от заданных условий хранения в стандартах или технических условиях на материал, узел или деталь.
Отдельные виды воздействия в пределах одного цикла могут совмещаться.
Съем образцов производят после окончания каждого цикла.
2.1.2. При наличии нескольких показателей испытания проводят по показателю, ответственному за работоспособность материала в изделии, или по каждому из выбранных показателей отдельно.
2.1.3. Узлы и детали не подвергают испытаниям на отдельные виды воздействия, указанные в п. 2.1, если имеются опытные данные по отсутствию влияния этих видов воздействия при хранении.
2.2.1. Отбор образцов проводят в соответствии с требованиями п. 1.2.1.
2.2.2. Минимальное количество узлов или деталей на один съем, требуемое для обеспечения необходимой статистической достоверности, должно быть указано в стандартах или технических условиях на метод определения их работоспособности в изделии.
2.3.1. Аппаратуру для испытаний выбирают в соответствии с требованиями п. 1.2.2.
2.4. Подготовка к испытаниям
2.4.1. Устанавливают наличие химического взаимодействия между материалом образца и влагой. Для этого в образце предварительно определяют количество химически связанной влаги. Затем образцы выдерживают при температуре (323±1) К (50±1) °С и заданной влажности воздуха не менее 20 сут и снова определяют количество химически связанной влаги.
Если количество химически связанной влаги в образцах после выдержки в указанных условиях меняется, считают, что материал образца в процессе старения химически взаимодействует с влагой.
За количество химически связанной влаги в образце принимают среднее арифметическое значение, определенное химическими методами не менее чем на пяти образцах по разности между общим содержанием влаги и физически связанной (свободной) влагой. (Например, общее содержание влаги определяют по методу Фишера, а содержание свободной влаги определяют высушиванием над фосфорным ангидридом в условиях, когда парциальное давление водяных паров близко к нулю, а температура и состав окружающей среды не приводят к возникновению химических реакций, при которых поглощается или выделяется вода или удаляются другие летучие соединения).
(Измененная редакция, Изм. № 1).
2.4.2. Составляют программу испытаний в соответствии с требованиями п. 1.2.3.1.
2.5. Проведение испытаний
2.5.1. Испытания, имитирующие воздействие положительной температуры и влажности воздуха, если исследуемый материал образца химически взаимодействует с влагой воздуха
2.5.1.1. Определяют исходное значение показателя в соответствии с требованиями п. 1.3.4.1.
2.5.1.2. Испытания проводят при температуре, установленной в соответствии с требованиями пп. 1.2.4.5 - 1.2.4.9. Температура испытания не должна быть ниже абсолютного максимума температуры хранения.
Влажность воздуха устанавливают в соответствии с требованиями п. 1.3.4.2, (режим 1).
2.5.1.4. Если экспериментальные данные описывают уравнениями 1 или 2 приложения 7, то продолжительность ускоренных испытаний tу по методу 2 при воздействии положительной температуры Ту, эквивалентную заданной продолжительности хранения и (или) эксплуатации tхр для каждого цикла испытаний, вычисляют по формуле (1), в которой Тп заменяют на Ту, а Е является коэффициентом температурной зависимости изменения показателя данного материала.
Если
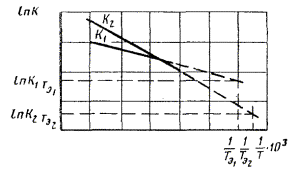
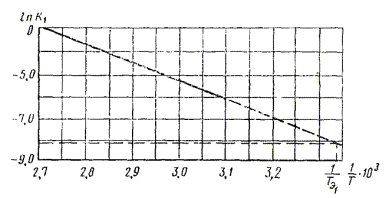
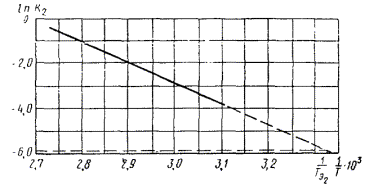
экспериментальные данные описывают уравнением (1) приложения 7 при К
= К1 + К2 и ![]() то tу
вычисляют по формуле
то tу
вычисляют по формуле
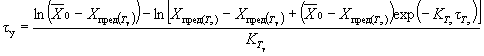 ,
,
где ![]() - исходное значение показателя по п. 1.3.4.1;
- исходное значение показателя по п. 1.3.4.1;
![]() - предельное
значение показателя при температуре ускоренных испытаний Ту;
- предельное
значение показателя при температуре ускоренных испытаний Ту;
![]() - предельное
значение показателя при эквивалентной температуре хранения Тэ;
- предельное
значение показателя при эквивалентной температуре хранения Тэ;
![]() - константа
скорости процесса изменения показателя при температуре ускоренных испытаний Ту;
- константа
скорости процесса изменения показателя при температуре ускоренных испытаний Ту;
![]() - константа
скорости процесса изменения показателя при эквивалентной температуре Тэ.
- константа
скорости процесса изменения показателя при эквивалентной температуре Тэ.
Если экспериментальные данные описывают уравнением (6) приложения 7, то tу вычисляют по формуле
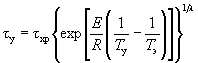 ,
,
где l определяют по пп. 6.1.4 - 6.1.5 приложения 7.
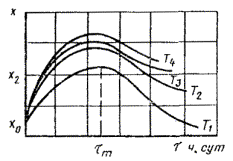
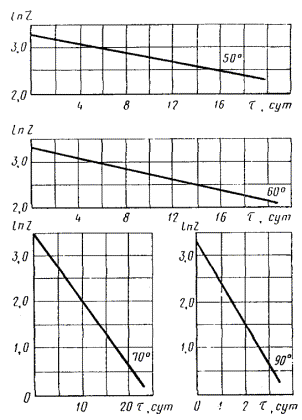
2.5.1.5. Если экспериментальные данные описывают уравнением 3, 4, 8 приложения 7, то по уравнениям 3, 4, 8 приложения 7 вычисляют значения показателя при Тэ и продолжительности хранения txp с градацией через каждые 365 сут, а также значения показателя при Ту и продолжительности ускоренных испытаний tу с градацией через каждые 10 сут. (Градация продолжительности ускоренных испытаний для расчета tу может быть изменена в зависимости от стойкости материала к термическому старению).
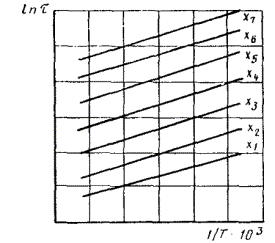
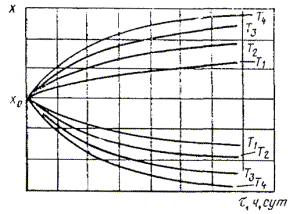
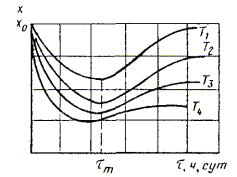
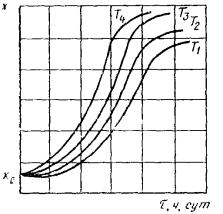
По полученным данным строят графики зависимости изменения показателя от txp и ty (черт. 4 и 5).
Черт. 4* Черт. 5
* Черт. 3 исключен (изм. № 1).
Если
задано предельно допустимое значение показателя Хдоп, то
отложив его на оси ординат, как показано на черт. 4 и 5, соединяют эти точки прямой,
параллельной оси абсцисс, и продолжают ее до пересечения с кривой ![]() (точка а).
Опустив из точки а
перпендикуляр на ось абсцисс, определяют продолжительность воздействия
положительной температуры tу при ускоренных испытаниях по
методу 2.
(точка а).
Опустив из точки а
перпендикуляр на ось абсцисс, определяют продолжительность воздействия
положительной температуры tу при ускоренных испытаниях по
методу 2.
Если
известна продолжительность хранения tхр, то для установления эквивалентной
продолжительности ускоренных испытаний из абсциссы tхр
восстанавливают перпендикуляр до пересечения с кривой ![]() (точка с),
проводят прямую линию, параллельную оси абсцисс из точки пересечения с кривой
(точка с),
проводят прямую линию, параллельную оси абсцисс из точки пересечения с кривой ![]() (точка b) и опускают из точки пересечения перпендикуляр на
ось абсцисс. Получают продолжительность воздействия положительной температуры
(точка b) и опускают из точки пересечения перпендикуляр на
ось абсцисс. Получают продолжительность воздействия положительной температуры ![]() при ускоренных
испытаниях по методу 2.
при ускоренных
испытаниях по методу 2.
Если на
графиках зависимости изменения показателя от продолжительности хранения и
ускоренных испытаний имеются экстремумы, и на каждой из кривых имеются два
значения tхр и tу, соответствующие ![]() ,
, ![]() определяют до точки
экстремума; если на каждой из кривых имеется только одно значение tхр и tу,
соответствующее
определяют до точки
экстремума; если на каждой из кривых имеется только одно значение tхр и tу,
соответствующее ![]() , то
, то ![]() определяют после
точки экстремума (черт. 6). При обработке экспериментальных данных на
электронной вычислительной машине (ЭВМ) tу вычисляют в соответствии с
алгоритмом, изложенным в приложении 14.
определяют после
точки экстремума (черт. 6). При обработке экспериментальных данных на
электронной вычислительной машине (ЭВМ) tу вычисляют в соответствии с
алгоритмом, изложенным в приложении 14.
2.5.1.6. При отсутствии возможности определения коэффициента Е по методу 1 продолжительность испытаний вычисляют по формуле (1), используя в качестве коэффициента Е его значение, полученное термогравиметрическим методом по ГОСТ 9.715-86, или Е материала-аналога.
Черт. 6
2.5.1.4 - 2.5.1.6 (Измененная редакция, Изм. № 1).
2.5.1.7. Проводят испытания в соответствии с требованиями пп. 1.2.4.2 - 1.2.4.15, если хранение осуществляют в герметичных условиях, или в соответствии с требованиями пп. 1.3.4.3 - 1.3.4.6, если хранение осуществляют в негерметичных условиях.
Если заданы конкретные условия хранения, то значение абсолютной влажности устанавливают, исходя из указанных условий хранения.
Если не заданы конкретные условия хранения, значение абсолютной влажности воздуха устанавливают q = (19,6±2,5) г/м3.
Продолжительность воздействия влаги устанавливают из условий достижения материалом образца массовой доли влаги, равной массовой доле влаги в образцах при хранении в течение предполагаемой продолжительности.
Массовую долю влаги в образцах определяют соответствующим физическим методом.
(Измененная редакция, Изм. № 1).
2.5.2. Испытания, имитирующие воздействие положительной температуры и влажности воздуха, если исследуемый материал образца химически не взаимодействует с влагой воздуха
Продолжительность выдержки устанавливают, исходя из условия достижения материалом образца постоянной массовой доли влаги, равной массовой доле влаги в образцах при хранении в течение предполагаемой продолжительности хранения.
2.5.2.2. В испытательной камере создают влажность воздуха и температуру, при которых в материале образца сохраняется постоянная массовая доля влаги. Метод определения влажности воздуха, при которой при заданной температуре по п. 2.5.1.2 сохраняется постоянная массовая доля влаги в материале образца, приведен в приложении 11.
(Измененная редакция, Изм. № 1).
2.5.2.3. Образцы, подготовленные по п. 2.5.2.1, помещают в испытательные камеры. Продолжительность испытаний устанавливают по пп. 2.5.1.4 - 2.5.1.6.
2.5.2.4. При установленном режиме испытаний в материале образца не должны происходить необратимые физические изменения, не имеющие места при хранении.
2.5.2.5. Если при заданной температуре испытаний в материале невозможно обеспечить постоянство массовой доли влаги, как указано в п. 2.5.2.1, то после испытаний его увлажняют до значения, определенного в соответствии с требованиями п. 2.5.1.8.
2.5.3. Испытания, имитирующие воздействие отрицательной температуры
2.5.3.1. Испытания на воздействие отрицательной температуры, имитирующие один год хранения в любом климатическом районе, проводят при температуре 213 К (минус 60 °С). Продолжительность испытаний 6 ч. Отсчет продолжительности испытаний начинают с момента достижения по всему объему образца температуры, отличающейся от заданной на 1 К (±1 °С).
Выдержку образцов при 293 К (20 °С) и 253 К (минус 20 °С) проводят до достижения по всему объему образца температуры, отличающейся от заданной на 1 К (±1 °С).
2.5.3.3. Испытания на воздействие отрицательной температуры, имитирующие один год хранения в заданных условиях, проводят при абсолютном минимуме температуры заданного климатического района. Продолжительность испытаний 6 ч.
2.5.4. Испытания, имитирующие воздействие перепадов температуры
2.5.4.1. Испытания на воздействие перепадов температуры, имитирующие один год хранения в любом климатическом районе, проводят при изменении температуры с переходом от 213 К (минус 60 °С) до 333 К (60 °С); охлаждение образцов до 213 К (минус 60 °С) и последующий нагрев до температуры 333 К (60 °С) проводят ступенчато с выдержкой при температурах 253 К (минус 20 °С) и 293 К (20 °С).
Продолжительность выдержки при указанных температурах устанавливают в соответствии с требованиями п. 2.5.3.2.
2.5.4.2. Испытания на воздействие перепадов температуры в заданных условиях хранения проводят при изменении температуры с переходом от абсолютного минимума до абсолютного максимума для заданного климатического района.
2.5.4.3. Количество переходов от 213 К (минус 60 °С) до 333 К (60 °С) или от абсолютного минимума до абсолютного максимума температуры устанавливают соответственно числу лет предполагаемого хранения. Если испытания проводят годовыми циклами, то испытания по п. 2.5.4 не проводят.
2.5.4.4. Если известно, что в условиях хранения в материале образца содержится несвязанная влага, то проводят испытания на воздействие перепадов температуры с переходом через 273 К (0 °С).
2.5.4.5. Наличие в материале образца несвязанной влаги устанавливают соответствующими физическими методами.
2.5.4.6. Испытания на воздействие перепадов температуры с переходом через 273 К (0 °С) проводят при изменении температуры от (263 - 258) К (минус 10 - минус 15) °С до (298±5) К (25±5) °С. Относительная влажность воздуха при положительной температуре должна быть не менее 70 %.
2.5.4.7. Один перепад температуры с переходом через 273 К (0 °С) имитируют выдержкой образцов в камере холода при (263 - 258) К (минус 10 - минус 15) °С и в камере тепла при (298±5) К (25±5) °С.
Выдержку образцов при указанных температурах проводят до достижения по всему объему образца температуры, отличающейся от заданной на ±1 К (±1 °С).
2.5.4.8. Один год предполагаемого хранения образцов под навесом имитируют количеством перепадов температуры, равным количеству переходов через 273 К (0 °С), установленным для заданного климатического района по ГОСТ 16350-80.
В случае хранения в неотапливаемых хранилищах количество перепадов температуры в зависимости от заданного климатического района и типа хранилища принимают равным количеству переходов температуры через 273 К (0 °С) в соответствии с приложением 12.
2.5.5. После окончания цикла испытаний, имитирующего воздействие климатических факторов, указанных в п. 2.1 за год, несколько лет или за всю предполагаемую продолжительность хранения, образцы извлекают из камер и проводят определение показателя в соответствии со стандартами на метод определения показателя.
Результаты испытаний записывают в протоколы, форма которых приведена в табл. 1 и 2 приложения 4.
Для узлов и деталей устанавливают соответствие испытуемых узлов или деталей требованиям стандартов или технических условий на их работоспособность в составе изделия.
(Измененная редакция, Изм. № 1).
2.6. Обработка результатов
2.6.1.
Если испытания проводили циклами, имитирующими воздействие климатических факторов
за каждый год хранения или несколько лет, то результаты испытаний, полученные
по п. 2.5.5,
обрабатывают в соответствии с рекомендуемым приложением 6 и строят график зависимости X или ![]() от продолжительности старения t (кривую прогноза), где
от продолжительности старения t (кривую прогноза), где
Xi - значение показателя, определенное по п. 2.5.5.
X0 - исходное значение показателя, определенное по п. 2.5.1.1.
По кривой прогноза определяют изменение показателя в течение предполагаемой продолжительности хранения.
2.6.2.
Если испытания проводили циклом, имитирующим воздействие климатических факторов
за всю предполагаемую продолжительность хранения, результат испытаний выражают
значениями X или ![]() ,
,
где X - значение показателя после предполагаемой продолжительности хранения, определенное по п. 2.5.5;
Х0 - исходное значение показателя, определенное по п. 2.5.1.1.
3. МЕТОД 3
3.1. Сущность метода заключается в одновременном проведении ускоренных испытаний исследуемого материала и материала-аналога на стойкость к воздействию климатических факторов и установлении сравнительной оценки стойкости материалов к указанному воздействию по изменению одного или нескольких характерных показателей старения.
3.2. Отбор образцов
3.2.1. Образцы исследуемого материала и материала-аналога должны соответствовать требованиям п. 1.2.1.
3.2.2. Образцы исследуемого материала и материала-аналога должны быть изготовлены по единой технологии.
3.3. Аппаратура
3.3.1. Аппаратура должна соответствовать требованиям, изложенным в п. 1.2.2.
3.4. Подготовка к испытаниям
3.4.1. Составляют программу испытаний в соответствии с требованиями п. 1.2.3.1.
3.4.2. Перед определением показателя до и после испытаний образцы кондиционируют в соответствии с требованиями пп. 1.3.3.2; 1.3.3.3.
3.5. Проведение испытаний
3.5.1. Определяют исходное значение показателя исследуемого материала и материала-аналога в соответствии со стандартами на метод определения показателя.
Испытания в режиме 1 проводят при температуре Tmах, установленной для данного материала в соответствии с требованиями пп. 1.2.4.7 - 1.2.4.9. Для узлов температуру испытаний устанавливают по п. 2.5.1.3.
Испытания в режиме 2 проводят при температуре T1, которая должна быть меньше Tmах на 20 К (20 °С).
Испытания в режиме 3, имитирующие воздействие перепадов температуры, проводят при изменении температуры с переходом от 213 К (минус 60 °С) до 333 К (60 °С).
3.5.3. Испытания исследуемых материалов по п. 3.5.2 проводят совместно с материалами-аналогами.
3.5.4. Испытания в режимах 1 и 2 проводят при постоянной абсолютной влажности воздуха q = (11,4±2,2) г/м3.
3.5.5. Образцы исследуемого материала и материала-аналога помещают в испытательные камеры после установления в них заданного режима испытаний. Испытания проводят непрерывно. Продолжительность вынужденных перерывов и условия хранения образцов при перерывах должны соответствовать требованиям п. 1.2.4.13.
3.5.6. Продолжительность испытаний при Tmах должна быть 30 сут, при t1 - 60 сут.
3.5.7. Испытания в режиме 3 проводят в соответствии с требованиями п. 2.5.4 и включают 20 перепадов температуры.
3.5.8. После окончания испытаний по всем режимам определяют значения показателей исследуемого материала и материала-аналога в соответствии со стандартами на метод определения показателя.
3.5.9. Результаты испытаний записывают в протокол по форме, приведенной в приложении 13.
3.6. Обработка результатов
3.6.1. Значения показателя исследуемого материала и материала-аналога в исходном состоянии и после испытаний по всем режимам принимают равным среднему арифметическому значению показателей образцов, испытанных в заданном режиме, которое вычисляют в соответствии с требованиями ГОСТ 269-66.
где ![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
,
![]() ,
, ![]() - соответственно
значения показателей исследуемого материала и материала-аналога после испытаний в
режиме 1;
- соответственно
значения показателей исследуемого материала и материала-аналога после испытаний в
режиме 1;
![]() ,
, ![]() - соответственно
значения показателей исследуемого материала и материала-аналога после испытаний
в режиме 2;
- соответственно
значения показателей исследуемого материала и материала-аналога после испытаний
в режиме 2;
Х0, Y0 - соответственно исходные значения показателей исследуемого материала и материала-аналога;
Тmax - температура испытаний в режиме 1, К;
t1 - температура испытаний в режиме 2, К;
Тэ - эквивалентная температура, установленная в соответствии с приложением 5, для Е материала-аналога, К.
В случае повышения значения показателя, сравнительную оценку стойкости исследуемого материала устанавливают, используя выражение
где ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
(Измененная редакция, Изм. № 1).
3.6.3. При выполнении неравенства (2) или (3) исследуемый материал по результатам испытаний в режимах 1 и 2 не уступает материалу-аналогу по стойкости к указанным воздействиям.
где Х0 и Х3 - соответственно значения показателя исследуемого материала до и после испытаний;
Y0 и Y3 - соответственно значения показателя материала-аналога до и после испытаний.
3.6.5. При выполнении неравенства (4) считают, что исследуемый материал по результатам испытаний в режиме 3 не уступает материалу-аналогу по стойкости к указанным воздействиям.
3.6.6. При совместном выполнении неравенств по пп. 3.6.2 и 3.6.4 считают, что исследуемый материал не уступает материалу-аналогу по стойкости к воздействию климатических факторов.
ПРИЛОЖЕНИЕ 1
Справочное
ТЕРМИНЫ, ПРИМЕНЯЕМЫЕ В СТАНДАРТЕ, И ПОЯСНЕНИЯ К НИМ
|
Термин |
Пояснение |
|
1. Характерный показатель старения |
|
|
2. Узел |
Неразъемное соединение, изготовленное из двух материалов, для которых в процессе испытаний не учитывают внутренние напряжения |
|
3. Деталь |
|
|
4. Слабое звено |
Элемент узла, характеризующийся минимальным запасом показателя после заданной продолжительности хранения |
|
5. Ненапряженное состояние |
Состояние материала, узла, детали при отсутствии внешних нагрузок |
|
6. Съем |
Отбор образцов из испытательной камеры или термостата после заданной продолжительности испытаний для определения показателя. Примечание. Количество образцов при каждом съеме должно обеспечивать попадание среднего арифметического значения показателя в доверительный интервал с заданной вероятностью |
|
7. Эквивалентная температура |
Условная температура, при которой константа скорости изменения характерного показателя при старении соответствует своему среднему значению при изменяющихся температурах в течение заданной продолжительности хранения |
|
8. Коэффициент Е, кДж/моль (ккал/моль) |
Коэффициент, характеризующий зависимость скорости изменения показателя от температуры при старении |
|
9. Массовая доля влаги |
По ГОСТ 8.221-76 |
|
10. Герметичные условия хранения |
Условия, обеспечивающие отсутствие массообмена с внешней средой |
|
11. Материал-аналог |
Материал, по которому имеются данные о стойкости к воздействию климатических факторов, аналогичный исследуемому материалу по назначению, составу, химическому строению и свойствам |
|
12. Термовлажностное климатическое старение |
Старение полимерного материала при воздействии температуры и паров воды |
(Измененная редакция, Изм. № 1).
ПРИЛОЖЕНИЕ 2
Рекомендуемое
ПРИМЕР ИЗГОТОВЛЕНИЯ ЗАГОТОВОК И ГРУППИРОВКИ ОБРАЗЦОВ НА КАЖДЫЙ СЪЕМ
1. Необходимо вычислить количество листов для изготовления заготовок и подобрать образцы для определения исходного значения показателя и на каждый съем.
Известно, что на один съем требуется 60 образцов; из одного листа можно вырезать 8 заготовок; из каждой заготовки можно вырезать 2 образца, количество съемов, с учетом определения исходного значения показателя, равно (7 + 1).
Количество листов для испытаний Q вычисляют по формуле
![]() .
.
2. Каждый из 30-ти листов разрезают на 8 равных частей и маркируют, как показано ниже.
|
1.1 |
|
2.1 |
|
3.1 |
… |
28.1 |
|
29.1 |
|
30.1 |
|
1.2 |
2.2 |
3.2 |
28.2 |
29.2 |
30.2 |
|||||
|
1.3 |
2.3 |
3.3 |
28.3 |
29.3 |
30.3 |
|||||
|
1.4 |
2.4 |
3.4 |
28.4 |
29.4 |
30.4 |
|||||
|
1.5 |
2.5 |
3.5 |
28.5 |
29.5 |
30.5 |
|||||
|
1.6 |
2.6 |
3.6 |
28.6 |
29.6 |
30.6 |
|||||
|
1.7 |
2.7 |
3.7 |
28.7 |
29.7 |
30.7 |
|||||
|
1.8 |
2.8 |
3.8 |
28.8 |
29.8 |
30.8 |
3. После маркировки листы разрезают на заготовки и по таблице подбирают их для определения исходного значения показателя и на каждый из съемов, как показано ниже.
|
Съем |
Номер образца |
||||||||||
|
I |
1.1 |
2.2 |
3.3 |
4.4 |
5.5 |
6.6 |
7.7 |
8.8 |
… |
29.7 |
30.8 |
|
II |
1.2 |
2.3 |
3.4 |
4.5 |
5.6 |
6.7 |
7.8 |
8.1 |
… |
29.8 |
30.1 |
|
III |
1.3 |
2.4 |
3.5 |
4.6 |
5.7 |
6.8 |
7.1 |
8.2 |
… |
29.1 |
30.2 |
|
IV |
1.4 |
2.5 |
3.6 |
4.7 |
5.8 |
6.1 |
7.2 |
8.3 |
… |
29.2 |
30.3 |
|
V |
1.5 |
2.6 |
3.7 |
4.8 |
5.1 |
6.2 |
7.3 |
8.4 |
… |
29.3 |
30.4 |
|
VI |
1.6 |
2.7 |
3.8 |
4.1 |
5.2 |
6.3 |
7.4 |
8.5 |
… |
29.4 |
30.5 |
|
VII |
1.7 |
2.8 |
3.1 |
4.2 |
5.3 |
6.4 |
7.5 |
8.6 |
… |
29.5 |
30.6 |
|
Исходный съем |
1.8 |
2.1 |
3.2 |
4.3 |
5.4 |
6.5 |
7.6 |
8.7 |
… |
29.6 |
30.7 |
ПРИЛОЖЕНИЕ 3
Обязательное
ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА ОБРАЗЦОВ ДЛЯ ИСПЫТАНИЙ
Количество образцов N, обеспечивающее определение среднего арифметического значения показателя (исходного значения и на каждый из съемов) с заданной относительной ошибкой и попадание ее в доверительный интервал с заданной вероятностью, вычисляют по формуле
где t - критерий распределения нормированных отклонений в малой выборке. Значение t определяют по таблице для испытанного количества образцов;
![]() - среднее
арифметическое значение коэффициента вариации отдельных значений показателя.
Значение
- среднее
арифметическое значение коэффициента вариации отдельных значений показателя.
Значение ![]() вычисляют в
соответствии с требованиями ГОСТ
269-66;
вычисляют в
соответствии с требованиями ГОСТ
269-66;
b - относительная ошибка измерения среднего арифметического значения показателя.
Значение b не должно превышать 5 %.
|
Количество образцов |
Значения t при доверительной вероятности |
||||
|
0,70 |
0,80 |
0,90 |
0,95 |
0,99 |
|
|
2 |
1,96 |
3,08 |
6,31 |
12,71 |
63,66 |
|
3 |
1,34 |
1,89 |
2,92 |
4,30 |
9,93 |
|
4 |
1,25 |
1,64 |
2,35 |
3,18 |
5,80 |
|
5 |
1,19 |
1,53 |
2,13 |
2,78 |
4,60 |
|
6 |
1,16 |
- |
2,02 |
2,57 |
4,03 |
|
7 |
1,13 |
1,44 |
1,94 |
2,45 |
3,70 |
|
8 |
- |
- |
1,90 |
2,37 |
3,50 |
|
9 |
- |
- |
1,86 |
2,30 |
3,36 |
|
10 |
1,10 |
1,38 |
1,83 |
2,26 |
3,25 |
|
12 |
- |
- |
1,80 |
2,20 |
3,11 |
|
14 |
- |
- |
1,77 |
2,18 |
3,16 |
|
15 |
1,08 |
1,35 |
1,76 |
2,16 |
3,06 |
|
16 |
- |
- |
1,75 |
2,13 |
2,95 |
|
18 |
- |
- |
1,74 |
2,11 |
2,90 |
|
20 |
- |
- |
1,73 |
2,09 |
2,86 |
|
25 |
- |
- |
1,71 |
2,06 |
2,80 |
|
30 |
1,06 |
1,31 |
1,70 |
2,04 |
2,76 |
|
35 |
- |
- |
1,69 |
2,03 |
2,73 |
|
40 |
- |
- |
1,68 |
2,02 |
2,70 |
|
50 |
- |
- |
1,68 |
2,01 |
2,68 |
|
60 |
1,05 |
1,30 |
1,67 |
2,00 |
2,66 |
|
120 |
1,04 |
1,29 |
1,66 |
1,98 |
2,62 |
|
¥ |
1,04 |
1,28 |
1,65 |
1,96 |
2,58 |
Если на один съем имеется меньше образцов, чем требуется по расчету, то устанавливают вероятность n попадания среднего арифметического значения показателя в доверительный интервал при имеющемся количестве образцов N.
Для этого
по формуле (1)
вычисляют значение критерия t и по
таблице определяют соответствующую ему доверительную вероятность. Коэффициент ![]() в этом случае
вычисляют по результатам испытаний не менее трех партий материала.
в этом случае
вычисляют по результатам испытаний не менее трех партий материала.
Количество образцов на 1 съем должно обеспечивать попадание среднего арифметического значения показателя в доверительный интервал с вероятностью не менее 0,7.
ПРИЛОЖЕНИЕ 4
Обязательное
СПОСОБ ПРОВЕРКИ СУЩЕСТВЕННОСТИ ИЗМЕНЕНИЯ ПОКАЗАТЕЛЯ
1. Определяют значение показателя в исходном состоянии и после каждого съема при испытаниях по настоящему стандарту. Результаты записывают в протокол по форме, приведенной в табл. 1.
Таблица 1
|
1 съем |
2 съем |
… |
10 съем |
|||||
|
Номер образца |
Значение показателя, Х0 |
Номер образца |
Значение показателя, Х1 |
Номер образца |
Значение показателя, Х2 |
… |
Номер образца |
Значение показателя, Х10 |
|
|
|
|
|
|
|
|
|
|
2. В соответствии с требованиями ГОСТ 269-66 вычисляют среднее арифметическое значение показателя, среднее квадратичное отклонение и коэффициент вариации отдельных значений показателя, границы доверительного интервала и относительное отклонение. Результаты записывают в протокол испытаний по форме, приведенной в табл. 2.
Таблица 2
|
Продолжительность старения t, сут |
Среднее арифметическое значение показателя |
Среднее квадратическое отклонение S |
Коэффициент вариации u |
Доверительный интервал ±DХ |
Относительное отклонение b |
1, 2. (Измененная редакция, Изм. № 1).
3. Существенность изменения показателя определяют после каждого съема путем проверки статистических гипотез о равенстве генеральных дисперсий и средних значений.
Данные для проверки статистических гипотез записывают в протокол испытаний по форме, приведенной в табл. 3.
Таблица 3
|
2-я выборка |
Гипотеза о равенстве дисперсии |
Гипотеза о равенстве средних значений |
|||||||
|
|
S1 |
n1 |
|
S2 |
n2 |
F |
Fтабл |
t |
tтабл |
|
|
|
|
|
|
|
|
|
|
|
3.1. Проверку гипотезы о равенстве генеральных дисперсий проводят по критерию Фишера, который вычисляют по формуле
![]() , (1)
, (1)
где ![]() и
и ![]() - соответственно большая и
меньшая из выборочных дисперсий.
- соответственно большая и
меньшая из выборочных дисперсий.
Значение F сравнивают с табличным значением
критерия Фишера Fтабл,
определенным для заданной вероятности и степеней свободы f1 = n1 - 1 (для
выборки с дисперсией ![]() ) и f2 = n2 - 1 (для
выборки с дисперсией
) и f2 = n2 - 1 (для
выборки с дисперсией ![]() ), где n1 и n2 -
количество образцов в каждой выборке.
), где n1 и n2 -
количество образцов в каждой выборке.
Значения Fтабл для доверительных вероятностей 0,75; 0,90; 0,95 и 0,99 приведены в табл. 4.
Если F < Fтабл гипотезу о равенстве генеральных дисперсий принимают; если F ³ Fтабл - отвергают.
(Измененная редакция, Изм. № 1).
3.2. Проверку гипотезы о равенстве средних значений проводят с помощью критерия Стъюдента t.
3.2.1. Если принята гипотеза о равенстве генеральных дисперсий, вычисляют t по формуле
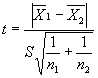 , (2)
, (2)
где S - сводная дисперсия, вычисляемая по формуле
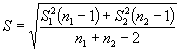 . (3)
. (3)
Полученное значение t сравнивают с tтабл, определенным при заданной доверительной вероятности и числе степеней свободы f = n1 + n2 - 2.
Значения критерия Стъюдента для различных доверительных вероятностей и различного числа степеней свободы приведены в табл. 5.
3.2.2. Если гипотеза о равенстве генеральных дисперсий отвергнута, то проверку гипотезы о равенстве средних значений проводят в соответствии с требованиями, изложенными ниже.
Таблица 4
|
Число степеней свободы для меньшей дисперсии |
Критерий Фишера (F) при числе степеней свободы для большей дисперсии |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
8 |
12 |
15 |
30 |
40 |
60 |
120 |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
0,75 |
1 |
5,83 |
7,50 |
8,20 |
8,58 |
8,82 |
8,98 |
9,19 |
9,41 |
9,49 |
9,67 |
9,71 |
9,76 |
9,80 |
|
2 |
2,57 |
3,00 |
3,15 |
3,23 |
3,28 |
3,31 |
3,35 |
3,39 |
3,41 |
3,44 |
3,45 |
3,46 |
3,47 |
|
|
3 |
2,02 |
2,28 |
2,36 |
2,39 |
2,41 |
2,42 |
2,44 |
2,45 |
2,46 |
2,47 |
2,47 |
2,47 |
2,47 |
|
|
4 |
1,81 |
2,00 |
2,05 |
2,06 |
2,07 |
2,08 |
2,08 |
2,08 |
2,08 |
2,08 |
2,08 |
2,08 |
2,08 |
|
|
5 |
1,69 |
1,85 |
1,88 |
1,89 |
1,89 |
1,89 |
1,89 |
1,89 |
1,89 |
1,88 |
1,87 |
1,87 |
1,87 |
|
|
6 |
1,62 |
1,76 |
1,78 |
1,79 |
1,79 |
1,78 |
1,77 |
1,77 |
1,76 |
1,75 |
1,75 |
1,74 |
1,74 |
|
|
7 |
1,57 |
1,70 |
1,72 |
1,72 |
1,71 |
1,71 |
1,70 |
1,68 |
1,68 |
1,66 |
1,66 |
1,65 |
1,65 |
|
|
8 |
1,54 |
1,66 |
1,67 |
1,66 |
1,66 |
1,65 |
1,64 |
1,62 |
1,62 |
1,60 |
1,59 |
1,59 |
1,58 |
|
|
9 |
1,51 |
1,62 |
1,63 |
1,63 |
1,62 |
1,61 |
1,60 |
1,58 |
1,57 |
1,55 |
1,55 |
1,54 |
1,53 |
|
|
10 |
1,49 |
1,60 |
1,60 |
1,59 |
1,59 |
1,58 |
1,56 |
1,54 |
1,53 |
1,51 |
1,51 |
1,50 |
1,49 |
|
|
11 |
1,47 |
1,58 |
1,58 |
1,57 |
1,56 |
1,55 |
1,53 |
1,51 |
1,50 |
1,48 |
1,47 |
1,47 |
1,46 |
|
|
12 |
1,46 |
1,56 |
1,56 |
1,55 |
1,54 |
1,53 |
1,51 |
1,49 |
1,48 |
1,45 |
1,45 |
1,44 |
1,43 |
|
|
13 |
1,45 |
1,54 |
1,54 |
1,53 |
1,52 |
1,51 |
1,49 |
1,47 |
1,46 |
1,43 |
1,42 |
1,42 |
1,41 |
|
|
14 |
1,44 |
1,53 |
1,53 |
1,52 |
1,51 |
1,50 |
1,48 |
1,45 |
1,44 |
1,41 |
1,41 |
1,40 |
1,39 |
|
|
15 |
1,43 |
1,52 |
1,52 |
1,51 |
1,49 |
1,48 |
1,46 |
1,44 |
1,43 |
1,40 |
1,39 |
1,38 |
1,37 |
|
|
16 |
1,42 |
1,51 |
1,51 |
1,50 |
1,48 |
1,48 |
1,46 |
1,44 |
1,41 |
1,38 |
1,37 |
1,36 |
1,35 |
|
|
17 |
1,42 |
1,51 |
1,50 |
1,49 |
1,47 |
1,46 |
1,44 |
1,41 |
1,40 |
1,37 |
1,36 |
1,35 |
1,34 |
|
|
18 |
1,41 |
1,50 |
1,49 |
1,48 |
1,46 |
1,45 |
1,43 |
1,40 |
1,39 |
1,36 |
1,35 |
1,34 |
1,33 |
|
|
19 |
1,41 |
1,49 |
1,49 |
1,47 |
1,46 |
1,44 |
1,42 |
1,40 |
1,38 |
1,35 |
1,34 |
1,33 |
1,32 |
|
|
20 |
1,40 |
1,49 |
1,48 |
1,46 |
1,45 |
1,44 |
1,42 |
1,39 |
1,37 |
1,34 |
1,33 |
1,32 |
1,31 |
|
|
22 |
1,40 |
1,48 |
1,47 |
1,45 |
1,44 |
1,42 |
1,40 |
1,37 |
1,36 |
1,32 |
1,31 |
1,30 |
1,30 |
|
|
24 |
1,39 |
1,47 |
1,46 |
1,44 |
1,43 |
1,41 |
1,39 |
1,36 |
1,35 |
1,31 |
1,30 |
1,29 |
1,28 |
|
|
26 |
1,38 |
1,46 |
1,45 |
1,44 |
1,42 |
1,41 |
1,39 |
1,35 |
1,34 |
1,30 |
1,29 |
1,28 |
1,26 |
|
|
28 |
1,38 |
1,46 |
1,45 |
1,43 |
1,41 |
1,40 |
1,38 |
1,34 |
1,33 |
1,29 |
1,28 |
1,27 |
1,25 |
|
|
30 |
1,38 |
1,45 |
1,44 |
1,42 |
1,41 |
1,39 |
1,37 |
1,34 |
1,32 |
1,28 |
1,27 |
1,26 |
1,24 |
|
|
40 |
1,36 |
1,44 |
1,42 |
1,40 |
1,39 |
1,37 |
1,35 |
1,31 |
1,30 |
1,25 |
1,24 |
1,22 |
1,21 |
|
|
60 |
1,35 |
1,42 |
1,41 |
1,38 |
1,37 |
1,35 |
1,32 |
1,29 |
1,27 |
1,22 |
1,21 |
1,19 |
1,17 |
|
|
120 |
1,34 |
1,40 |
1,39 |
1,37 |
1,35 |
1,33 |
1,30 |
1,26 |
1,24 |
1,19 |
1,18 |
1,16 |
1,13 |
|
|
¥ |
1,32 |
1,39 |
1,37 |
1,35 |
1,33 |
1,31 |
1,28 |
1,24 |
1,22 |
1,16 |
1,14 |
1,12 |
1,08 |
|
|
0,90 |
1 |
39,9 |
49,5 |
53,6 |
55,8 |
57,2 |
58,2 |
59,4 |
60,7 |
61,2 |
62,3 |
62,5 |
62,8 |
63,1 |
|
2 |
8,53 |
9,00 |
9,16 |
9,24 |
9,29 |
9,33 |
9,37 |
9,41 |
9,42 |
9,46 |
9,47 |
9,47 |
9,48 |
|
|
3 |
5,54 |
5,46 |
5,39 |
5,34 |
5,31 |
5,28 |
5,25 |
5,22 |
5,20 |
5,17 |
5,16 |
5,15 |
5,13 |
|
|
4 |
4,54 |
4,32 |
4,19 |
4,11 |
4,05 |
4,01 |
3,95 |
3,90 |
3,87 |
3,82 |
3,80 |
3,79 |
3,78 |
|
|
5 |
4,06 |
3,78 |
3,62 |
3,52 |
3,45 |
3,40 |
3,34 |
3,27 |
3,24 |
3,17 |
3,16 |
3,14 |
3,12 |
|
|
6 |
3,78 |
3,46 |
3,29 |
3,18 |
3,11 |
3,05 |
2,98 |
2,90 |
2,87 |
2,80 |
2,78 |
2,76 |
2,74 |
|
|
7 |
3,59 |
3,26 |
3,07 |
2,96 |
2,88 |
2,83 |
2,75 |
2,67 |
2,63 |
2,56 |
2,54 |
2,51 |
2,49 |
|
|
8 |
3,46 |
3,11 |
2,92 |
2,81 |
2,73 |
2,07 |
2,59 |
2,50 |
2,46 |
2,38 |
2,36 |
2,34 |
2,32 |
|
|
9 |
3,36 |
3,01 |
2,81 |
2,69 |
2,61 |
2,55 |
2,47 |
2,38 |
2,34 |
2,25 |
2,23 |
2,21 |
2,18 |
|
|
10 |
3,28 |
2,92 |
2,73 |
2,61 |
2,52 |
2,46 |
2,38 |
2,28 |
2,24 |
2,16 |
2,13 |
2,11 |
2,08 |
|
|
11 |
3,23 |
2,86 |
2,66 |
2,54 |
2,45 |
2,39 |
2,30 |
2,21 |
2,17 |
2,08 |
2,05 |
2,03 |
2,00 |
|
|
12 |
3,18 |
2,81 |
2,61 |
2,48 |
2,39 |
2,33 |
2,24 |
2,15 |
2,10 |
2,01 |
1,99 |
1,96 |
1,93 |
|
|
13 |
3,14 |
2,76 |
2,56 |
2,43 |
2,35 |
2,28 |
2,20 |
2,10 |
2,05 |
1,96 |
1,93 |
1,90 |
1,88 |
|
|
14 |
3,10 |
2,73 |
2,52 |
2,39 |
2,31 |
2,24 |
2,15 |
2,05 |
2,01 |
1,91 |
1,89 |
1,86 |
1,82 |
|
|
15 |
3,07 |
2,70 |
2,49 |
2,36 |
2,27 |
2,21 |
2,12 |
2,02 |
1,97 |
1,87 |
1,85 |
1,82 |
1,79 |
|
|
16 |
3,05 |
2,67 |
2,46 |
2,33 |
2,24 |
2,18 |
2,09 |
1,99 |
1,94 |
1,84 |
1,81 |
1,79 |
1,75 |
|
|
17 |
3,03 |
2,64 |
2,44 |
2,31 |
2,22 |
2,15 |
2,06 |
1,96 |
1,91 |
1,81 |
1,78 |
1,75 |
1,72 |
|
|
18 |
3,01 |
2,62 |
2,42 |
2,29 |
2,20 |
2,13 |
2,04 |
1,93 |
1,89 |
1,78 |
1,75 |
1,72 |
1,69 |
|
|
19 |
2,99 |
2,61 |
2,40 |
2,27 |
2,18 |
2,11 |
2,02 |
1,91 |
1,86 |
1,70 |
1,73 |
1,70 |
1,67 |
|
|
20 |
2,97 |
2,59 |
2,38 |
2,25 |
2,16 |
2,09 |
2,00 |
1,89 |
1,84 |
1,74 |
1,71 |
1,68 |
1,64 |
|
|
22 |
2,95 |
2,56 |
2,35 |
2,22 |
2,13 |
2,06 |
1,97 |
1,80 |
1,81 |
1,70 |
1,67 |
1,64 |
1,60 |
|
|
24 |
2,93 |
2,54 |
2,33 |
2,19 |
2,10 |
2,04 |
1,94 |
1,83 |
1,78 |
1,67 |
1,64 |
1,61 |
1,57 |
|
|
26 |
2,91 |
2,52 |
2,31 |
2,17 |
2,08 |
2,01 |
1,92 |
1,81 |
1,76 |
1,65 |
1,61 |
1,58 |
1,54 |
|
|
28 |
2,89 |
2,50 |
2,29 |
2,16 |
2,06 |
2,00 |
1,90 |
1,79 |
1,74 |
1,63 |
1,59 |
1,56 |
1,52 |
|
|
30 |
2,88 |
2,49 |
2,28 |
2,14 |
2,05 |
1,98 |
1,88 |
1,77 |
1,72 |
1,61 |
1,57 |
1,54 |
1,50 |
|
|
40 |
2,84 |
2,44 |
2,23 |
2,08 |
2,00 |
1,93 |
1,83 |
1,71 |
1,66 |
1,54 |
1,51 |
1,47 |
1,42 |
|
|
60 |
2,79 |
2,39 |
2,18 |
2,04 |
1,95 |
1,87 |
1,77 |
1,66 |
1,60 |
1,48 |
1,44 |
1,40 |
1,35 |
|
|
120 |
2,75 |
2,35 |
2,13 |
1,99 |
1,90 |
1,82 |
1,72 |
1,60 |
1,55 |
1,41 |
1,37 |
1,32 |
1,26 |
|
|
¥ |
2,71 |
2,30 |
2,08 |
1,94 |
1,85 |
1,77 |
1,67 |
1,55 |
1,49 |
1,34 |
1,30 |
1,24 |
1,17 |
|
|
0,95 |
1 |
161,0 |
200,0 |
216,0 |
225,0 |
230,0 |
234,0 |
239,0 |
244,0 |
246,0 |
250,0 |
251,0 |
252,0 |
253,0 |
|
2 |
16,5 |
19,0 |
19,2 |
19,2 |
19,3 |
19,3 |
19,4 |
19,4 |
19,4 |
19,5 |
19,5 |
19,5 |
19,5 |
|
|
3 |
10,10 |
9,55 |
9,28 |
9,28 |
9,10 |
8,94 |
8,85 |
8,74 |
8,70 |
8,62 |
8,59 |
8,57 |
8,55 |
|
|
4 |
7,71 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,04 |
5,91 |
5,86 |
5,75 |
5,72 |
5,69 |
5,66 |
|
|
5 |
6,61 |
5,79 |
5,41 |
5,19 |
5,05 |
4,95 |
4,82 |
4,68 |
4,62 |
4,50 |
4,46 |
4,43 |
4,40 |
|
|
6 |
5,99 |
5,14 |
4,76 |
4,53 |
4,39 |
4,28 |
4,15 |
4,00 |
3,94 |
3,81 |
3,77 |
3,74 |
3,70 |
|
|
7 |
5,39 |
4,74 |
4,35 |
4,12 |
3,97 |
3,87 |
3,73 |
3,57 |
3,51 |
3,38 |
3,34 |
3,30 |
3,27 |
|
|
8 |
5,32 |
4,46 |
4,07 |
3,84 |
3,69 |
3,58 |
3,44 |
3,28 |
3,22 |
3,08 |
3,04 |
3,01 |
2,97 |
|
|
9 |
5,12 |
4,26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,23 |
3,07 |
3,01 |
2,86 |
2,83 |
2,79 |
2,75 |
|
|
10 |
4,96 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,07 |
2,91 |
2,85 |
2,70 |
2,66 |
2,62 |
2,58 |
|
|
11 |
4,84 |
3,98 |
3,59 |
3,36 |
3,20 |
3,09 |
2,95 |
2,79 |
2,72 |
2,57 |
2,53 |
2,49 |
2,45 |
|
|
12 |
4,75 |
3,89 |
3,49 |
3,26 |
3,11 |
3,00 |
2,85 |
2,69 |
2,62 |
2,47 |
2,43 |
2,38 |
2,34 |
|
|
13 |
4,67 |
3,81 |
3,41 |
3,18 |
3,03 |
2,92 |
2,77 |
2,60 |
2,53 |
2,38 |
2,34 |
2,30 |
2,25 |
|
|
14 |
4,60 |
3,74 |
3,34 |
3,11 |
2,96 |
2,85 |
2,70 |
2,53 |
2,46 |
2,31 |
2,27 |
2,22 |
2,18 |
|
|
15 |
4,54 |
3,68 |
3,29 |
3,06 |
2,90 |
2,79 |
2,64 |
2,48 |
2,40 |
2,25 |
2,20 |
2,16 |
2,11 |
|
|
16 |
4,49 |
3,63 |
3,24 |
3,01 |
2,85 |
2,74 |
2,59 |
2,42 |
2,35 |
2,19 |
2,15 |
2,11 |
2,06 |
|
|
17 |
4,45 |
3,59 |
3,20 |
2,96 |
2,81 |
2,70 |
2,55 |
2,38 |
2,31 |
2,15 |
2,10 |
2,06 |
2,01 |
|
|
18 |
4,41 |
3,55 |
3,16 |
2,93 |
2,77 |
2,66 |
2,51 |
2,34 |
2,27 |
2,11 |
2,06 |
2,02 |
1,97 |
|
|
19 |
4,38 |
3,52 |
3,13 |
2,90 |
2,74 |
2,63 |
2,48 |
2,31 |
2,23 |
2,07 |
2,03 |
1,98 |
1,93 |
|
|
20 |
4,35 |
3,49 |
3,10 |
2,87 |
2,71 |
2,60 |
2,45 |
2,28 |
2,20 |
2,04 |
1,99 |
1,95 |
1,90 |
|
|
22 |
4,30 |
3,44 |
3,05 |
2,82 |
2,66 |
2,55 |
2,40 |
2,23 |
2,15 |
1,98 |
1,94 |
1,89 |
1,84 |
|
|
24 |
4,26 |
3,40 |
3,01 |
2,78 |
2,62 |
2,51 |
2,36 |
2,18 |
2,11 |
1,94 |
1,89 |
1,84 |
1,79 |
|
|
26 |
4,23 |
3,37 |
2,98 |
2,74 |
2,59 |
2,47 |
2,32 |
2,15 |
2,07 |
1,90 |
1,85 |
1,80 |
1,75 |
|
|
28 |
4,20 |
3,34 |
2,95 |
2,71 |
2,56 |
2,45 |
2,29 |
2,12 |
2,04 |
1,87 |
1,82 |
1,77 |
1,71 |
|
|
30 |
4,17 |
3,32 |
2,92 |
2,69 |
2,53 |
2,42 |
2,27 |
2,09 |
2,01 |
1,84 |
1,79 |
1,74 |
1,68 |
|
|
40 |
4,08 |
3,23 |
2,84 |
2,61 |
2,45 |
2,34 |
2,18 |
2,00 |
1,92 |
1,74 |
1,69 |
1,64 |
1,58 |
|
|
60 |
4,00 |
3,15 |
2,76 |
2,53 |
2,37 |
2,25 |
2,10 |
1,92 |
1,84 |
1,65 |
1,59 |
1,53 |
1,47 |
|
|
120 |
3,92 |
3,07 |
2,68 |
2,45 |
2,29 |
2,17 |
2,02 |
1,83 |
1,75 |
1,55 |
1,50 |
1,43 |
1,35 |
|
|
¥ |
3,84 |
3,00 |
2,60 |
2,37 |
2,21 |
2,10 |
1,94 |
1,75 |
1,67 |
1,46 |
1,39 |
1,32 |
1,22 |
|
|
0,99 |
2 |
98,5 |
99,0 |
99,2 |
99,2 |
99,3 |
99,3 |
99,4 |
99,4 |
99,4 |
99,5 |
99,5 |
99,5 |
99,5 |
|
3 |
34,1 |
30,8 |
29,5 |
28,7 |
28,2 |
27,9 |
27,5 |
27,1 |
26,9 |
26,5 |
26,4 |
26,3 |
26,2 |
|
|
4 |
21,2 |
18,0 |
16,7 |
16,0, |
15,5 |
15,2 |
14,8 |
14,4 |
14,2 |
13,8 |
13,7 |
13,7 |
13,6 |
|
|
5 |
16,3 |
13,3 |
12,1 |
11,4 |
11,0 |
10,7 |
10,3 |
9,89 |
9,72 |
9,38 |
9,29 |
9,20 |
9,11 |
|
|
6 |
13,7 |
10,9 |
9,78 |
9,15 |
8,75 |
8,47 |
8,10 |
7,72 |
7,56 |
7,23 |
7,14 |
7,06 |
6,97 |
|
|
7 |
12,2 |
9,55 |
8,45 |
7,85 |
7,46 |
7,19 |
6,84 |
6,47 |
6,31 |
5,99 |
5,91 |
5,82 |
5,74 |
|
|
8 |
11,3 |
8,65 |
7,59 |
7,01 |
6,63 |
6,37 |
6,03 |
5,67 |
5,52 |
5,20 |
5,12 |
5,03 |
4,95 |
|
|
9 |
10,6 |
8,02 |
6,99 |
6,42 |
6,06 |
5,80 |
5,47 |
5,11 |
4,96 |
4,65 |
4,57 |
4,48 |
4,40 |
|
|
10 |
10,0 |
7,56 |
6,55 |
5,99 |
5,64 |
5,39 |
5,06 |
4,71 |
4,56 |
4,25 |
4,17 |
4,08 |
4,00 |
|
|
11 |
9,65 |
7,21 |
6,22 |
5,67 |
5,32 |
5,07 |
4,74 |
4,40 |
4,25 |
3,94 |
3,86 |
3,81 |
3,69 |
|
|
12 |
9,33 |
6,93 |
5,95 |
5,41 |
5,06 |
4,82 |
4,50 |
4,16 |
4,01 |
3,70 |
3,62 |
3,57 |
3,45 |
|
|
13 |
9,07 |
6,70 |
5,74 |
5,21 |
4,86 |
4,62 |
4,30 |
3,96 |
3,82 |
3,51 |
3,43 |
3,38 |
3,25 |
|
|
14 |
8,86 |
6,51 |
5,56 |
5,04 |
4,69 |
4,46 |
4,14 |
3,80 |
3,66 |
3,35 |
3,27 |
3,22 |
3,09 |
|
|
15 |
8,68 |
6,36 |
5,42 |
4,89 |
4,56 |
4,32 |
4,00 |
3,67 |
3,52 |
3,21 |
3,13 |
3,08 |
2,96 |
|
|
16 |
8,53 |
6,23 |
5,29 |
4,77 |
4,44 |
4,20 |
3,89 |
3,55 |
3,41 |
3,10 |
3,02 |
2,97 |
2,84 |
|
|
17 |
8,40 |
6,11 |
5,18 |
4,67 |
4,34 |
4,10 |
3,79 |
3,46 |
3,31 |
3,00 |
2,92 |
2,87 |
2,75 |
|
|
18 |
8,29 |
6,01 |
5,09 |
4,58 |
4,25 |
4,01 |
3,71 |
3,37 |
3,23 |
2,92 |
2,84 |
2,78 |
2,66 |
|
|
19 |
8,18 |
5,93 |
5,01 |
4,50 |
4,17 |
3,94 |
3,63 |
3,30 |
3,15 |
2,84 |
2,76 |
2,71 |
2,58 |
|
|
20 |
8,10 |
5,85 |
4,94 |
4,43 |
4,10 |
3,87 |
3,56 |
3,23 |
3,09 |
2,78 |
2,69 |
2,64 |
2,52 |
|
|
22 |
7,95 |
5,72 |
4,82 |
4,31 |
3,99 |
3,76 |
3,45 |
3,12 |
2,98 |
2,67 |
2,58 |
2,53 |
2,40 |
|
|
24 |
7,82 |
5,61 |
4,72 |
4,22 |
3,90 |
3,67 |
3,36 |
3,03 |
2,89 |
2,58 |
2,49 |
2,40 |
2,31 |
|
|
26 |
7,72 |
5,53 |
4,64 |
4,14 |
3,82 |
3,59 |
3,29 |
2,96 |
2,81 |
2,50 |
2,42 |
2,33 |
2,23 |
|
|
28 |
7,64 |
5,45 |
4,57 |
4,07 |
3,75 |
3,53 |
3,23 |
2,90 |
2,75 |
2,44 |
2,35 |
2,26 |
2,17 |
|
|
30 |
7,56 |
5,39 |
4,51 |
4,02 |
3,70 |
3,47 |
3,17 |
2,84 |
2,70 |
2,39 |
2,30 |
2,21 |
2,11 |
|
|
40 |
7,31 |
5,18 |
4,31 |
3,83 |
3,51 |
3,29 |
2,99 |
2,66 |
2,52 |
2,20 |
2,11 |
2,02 |
1,92 |
|
|
60 |
7,08 |
4,98 |
4,13 |
3,65 |
3,34 |
3,12 |
2,82 |
2,50 |
2,35 |
2,03 |
1,94 |
1,84 |
1,73 |
|
|
120 |
6,85 |
4,79 |
3,95 |
3,48 |
3,17 |
2,96 |
2,66 |
2,34 |
2,19 |
1,86 |
1,76 |
1,66 |
1,53 |
|
|
¥ |
6,63 |
4,61 |
3,78 |
3,32 |
3,02 |
2,80 |
2,51 |
2,18 |
2,04 |
1,70 |
1,59 |
1,47 |
1,32 |
|
(Измененная редакция, Изм. № 1).
Таблица 5
|
Критерий Стъюдента t при доверительной вероятности n |
|||||||
|
0,050 |
0,750 |
0,900 |
0,950 |
0,975 |
0,990 |
0,995 |
|
|
1 |
1,000 |
2,414 |
6,314 |
12,706 |
25,452 |
63,657 |
127,320 |
|
2 |
0,817 |
1,604 |
2,920 |
4,303 |
6,205 |
9,925 |
14,089 |
|
3 |
0,765 |
1,423 |
2,353 |
3,183 |
4,177 |
5,841 |
7,453 |
|
4 |
0,741 |
1,344 |
2,132 |
2,776 |
3,495 |
4,604 |
5,598 |
|
5 |
0,727 |
1,301 |
2,015 |
2,571 |
3,163 |
4,032 |
4,773 |
|
6 |
0,718 |
1,273 |
1,943 |
2,447 |
2,969 |
3,707 |
4,317 |
|
7 |
0,711 |
1,254 |
1,895 |
2,365 |
2,841 |
3,500 |
4,029 |
|
8 |
0,706 |
1,240 |
1,860 |
2,306 |
2,752 |
3,355 |
3,833 |
|
9 |
0,703 |
1,230 |
1,833 |
2,262 |
2,685 |
3,250 |
3,690 |
|
10 |
0,700 |
1,221 |
1,813 |
2,2:28 |
2,634 |
3,169 |
3,581 |
|
11 |
0,697 |
1,215 |
1,796 |
2,201 |
2,593 |
3,106 |
3,497 |
|
12 |
0,695 |
1,209 |
1,782 |
2,179 |
2,560 |
3,055 |
3,428 |
|
13 |
0,694 |
1,204 |
1,771 |
2,160 |
2,533 |
3,012 |
3,373 |
|
14 |
0,692 |
1,200 |
1,761 |
2,145 |
2,510 |
2,977 |
3,326 |
|
15 |
0,691 |
1,197 |
1,753 |
2,132 |
2,490 |
2,947 |
3,286 |
|
16 |
0,690 |
1,194 |
1,746 |
2,120 |
2,473 |
2,921 |
3,252 |
|
17 |
0,689 |
1,191 |
1,740 |
2,110 |
2,458 |
2,898 |
3,223 |
|
18 |
0,688 |
1,189 |
1,734 |
2,101 |
2,445 |
2,878 |
3,197 |
|
19 |
0,688 |
1,187 |
1,729 |
2,093 |
2,433 |
2,861 |
3,174 |
|
20 |
0,687 |
1,185 |
1,725 |
2,086 |
2,423 |
2,845 |
3,153 |
|
21 |
0,686 |
1,183 |
1,721 |
2,080 |
2,414 |
2,831 |
3,125 |
|
22 |
0,686 |
1,182 |
1,720 |
2,074 |
2,406 |
2,819 |
3,119 |
|
23 |
0,685 |
1,180 |
1,717 |
2,069 |
2,398 |
2,807 |
3,104 |
|
24 |
0,685 |
1,179 |
1,711 |
2,064 |
2,392 |
2,797 |
3,091 |
|
25 |
0,684 |
1,178 |
1,708 |
2,060 |
2,385 |
2,787 |
3,078 |
|
26 |
0,684 |
1,177 |
1,706 |
2,056 |
2,379 |
2,779 |
3,067 |
|
27 |
0,683 |
1,176 |
1,703 |
2,052 |
2,373 |
2,771 |
3,057 |
|
28 |
0,683 |
1,175 |
1,701 |
2,048 |
2,369 |
2,763 |
3,047 |
|
29 |
0,683 |
1,174 |
1,699 |
2,045 |
2,364 |
2,756 |
3,038 |
|
30 |
0,683 |
1,173 |
1,697 |
2,042 |
2,360 |
2,750 |
3,030 |
|
40 |
0,681 |
1,167 |
1,684 |
2,021 |
2,329 |
2,705 |
2,971 |
|
60 |
0,679 |
1,162 |
1,671 |
2,000 |
2,299 |
2,660 |
2,915 |
|
120 |
0,677 |
1,156 |
1,658 |
1,980 |
2,270 |
2,617 |
2,860 |
|
¥ |
0,674 |
1,150 |
1,645 |
1,960 |
2,241 |
2,575 |
2,807 |
Критерий t вычисляют по формуле
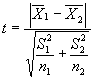 , (4)
, (4)
и сравнивают его с приближенным критерием Стъюдента tпр, вычисленным по формуле
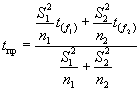 , (5)
, (5)
где ![]() и
и ![]() устанавливают
по табл. 5
для заданной доверительной вероятности n и числе степеней свободы f1 = n1 - 1 и f2 = n2 - 1
соответственно.
устанавливают
по табл. 5
для заданной доверительной вероятности n и числе степеней свободы f1 = n1 - 1 и f2 = n2 - 1
соответственно.
3.3. Если t < tтабл или t < tпр гипотезу о равенстве средних значений принимают. При этом расхождения между средними значениями считают случайными и не обусловленными старением материала при испытаниях, а изменение показателя считают не существенным.
Если t > tтабл или t > tпр, гипотезу отвергают; расхождения между средними значениями считают неслучайными и обусловленными старением материала при испытаниях, а изменение показателя - существенным.
ПРИЛОЖЕНИЕ 5
Обязательное
ОПРЕДЕЛЕНИЕ ЭКВИВАЛЕНТНОЙ ТЕМПЕРАТУРЫ Tэ
1. Эквивалентную температуру Тэ определяют по номограмме, приведенной на чертеже, или вычисляют по формуле
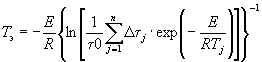 ,
,
где Е - коэффициент, кДж/моль (ккал/моль);
R - универсальная газовая постоянная, равная 8,314 Дж/моль×К (1,987 ккал/моль×К);
t0 - среднестатистическое количество часов заданной продолжительности хранения;
![]() - продолжительность
существования интервала температуры (не более 5 °С) со средней температурой Тj, ч;
- продолжительность
существования интервала температуры (не более 5 °С) со средней температурой Тj, ч;
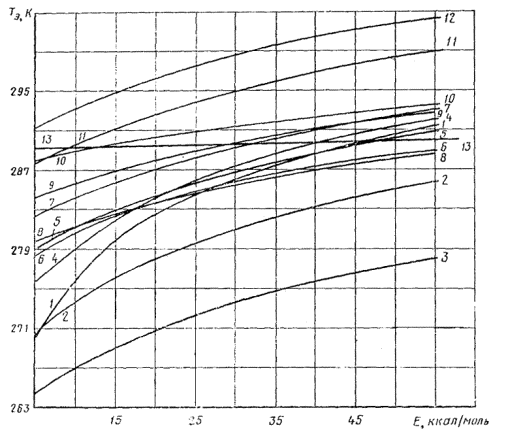
1 - очень холодный; 2 - холодный; 3 - арктический западный; 4 - умеренно холодный; 5 - умеренный; 6 - умеренно влажный; 7 - умеренно теплый; 8 - умеренно теплый влажный; 9 - умеренно теплый с мягкой зимой; 10 - теплый влажный; 11 - жаркий сухой; 12 - очень жаркий сухой; 13 - отапливаемое хранилище
п - количество интервалов температуры со средней температурой Тj.
2. На номограмме приведена зависимость Тэ от Е для климатических районов по ГОСТ 16350-80 и отапливаемого хранилища.
Для других условий хранения эквивалентную температуру вычисляют по данным распределения температуры в заданных условиях, статистически обработанным за период наблюдения не менее 5 лет.
3. Пример вычисления Тэ
3.1. По результатам испытаний установлено значение Е = 104,67×103 Дм/моль (25 ккал/моль).
3.2. Для климатического района установлено распределение температуры в течение года от 253,1 К (минус 19,9 °С) до 318 К (45 °С) интервалами в 5 К (5 °С).
Для каждого интервала вычисляют температуру Tj, как среднее арифметическое значение нижнего и верхнего значений температуры каждого интервала. Данные приведены в таблице.
По данным таблицы вычисляют:
t0 по формуле
![]() значение
значение 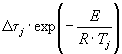 на каждом интервале:
на каждом интервале:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
|
Номер интервала п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
Интервал температуры, °С |
От - 19,9 до - 15,0 |
От - 14,9 до - 10,0 |
От - 9,9 до -5,0 |
От - 4,9 до 50,0 |
От 0,1 до 5,0 |
От 5,1 до 10,0 |
От 10,1 до 15,0 |
От 15,1 до 20,0 |
От 20,1 до 25,0 |
От 25,1 до 30,0 |
От 30,1 до 35,0 |
От 35,1 до 40,0 |
От 40,1 до 45,0 |
|
Средняя температура Тj интервала, К. |
255,5 |
260,5 |
265,5 |
270,5 |
275,5 |
280,5 |
285,5 |
290,5 |
295,5 |
300,5 |
305,5 |
310,5 |
315,5 |
|
Продолжительность существования интервала Dtj, ч |
3 |
30 |
139 |
491 |
1069 |
1203 |
1068 |
1014 |
1195 |
1339 |
793 |
391 |
32 |
11) ![]()
12) ![]()
13) ![]()
сумму
значений 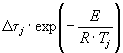
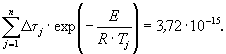
3.3. Вычисляют эквивалентную температуру (Тэ) по формуле
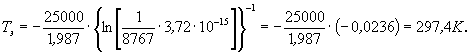
Приложение 5. (Измененная редакция, Изм. № 1).
ПРИЛОЖЕНИЕ 6
Рекомендуемое
ОПИСАНИЕ КИНЕТИЧЕСКОЙ ЗАВИСИМОСТИ ИЗМЕНЕНИЯ ПОКАЗАТЕЛЯ ОТ ПРОДОЛЖИТЕЛЬНОСТИ СТАРЕНИЯ ОБРАТНЫМ ПОЛИНОМОМ ВТОРОЙ СТЕПЕНИ
Экспериментальные зависимости изменения показателя Х(tij) от продолжительности ускоренных испытаний tij при каждой температуре обрабатывают методом наименьших квадратов с использованием полинома 2-й степени вида
![]() ,
,
где i - порядковый номер температуры испытаний, i = 1, 2, 3, ..., п, п - число температур испытаний;
j - порядковый номер съема образцов, j = 1, 2, 3, ..., mi, mi - число съемов при каждой температуре.
Обратный полином второй степени имеет вид
![]() .
.
Константы a0, a1, a2 вычисляют по формулам:
![]() ;
;
![]() ;
;
![]() ,
,
где ![]() ;
; 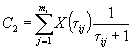 ;
; 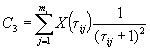 ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Приложение 6. (Измененная редакция, Изм. № 1).
ПРИЛОЖЕНИЕ 7
Рекомендуемое
АНАЛИТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ
1. Если изменение показателя происходит до некоторого предельного значения Хпред, не зависящего от температуры испытаний, то кинетические кривые зависимости X от t описывают уравнением первого порядка типа
где Х0, Хпред - соответственно исходное и предельное значения показателя;
X, X(t) - значения показателя в момент времени t;
К - константа скорости процесса.
Для проверки правомерности применения уравнения (1) и определения значений К и Хпред при каждой температуре, результаты испытаний обрабатывают в соответствии с требованиями, изложенными ниже.
Черт. 1
Черт. 2
1.1. По результатам испытаний, полученным по методу 1 настоящего стандарта при температурах Т1, Т2, Т3, ..., Тп, где п ³ 4, строят кривые кинетической зависимости X от t, как показано на черт. 1.
1.2. Способом графического дифференцирования, приведенным в
справочном приложении 8, определяют значения производных ![]() во всем диапазоне
изменения показателя Хi при каждой из температур.
во всем диапазоне
изменения показателя Хi при каждой из температур.
1.3. Строят график зависимости ![]() от Xi
для каждой из температур.
Линейность графиков, не проходящих через начало координат, является критерием
правомерности описания полученных кинетических кривых уравнением (1).
от Xi
для каждой из температур.
Линейность графиков, не проходящих через начало координат, является критерием
правомерности описания полученных кинетических кривых уравнением (1).
Примечание. Здесь и далее по тексту графики зависимостей строят методом наименьших квадратов.
1.4. Экстраполируют график зависимости ![]() от Х на
значение
от Х на
значение ![]() , как показано на черт. 2, и
определяют Хпред по отрезку, отсекаемому этой
прямой на оси абсцисс; константу К
- по тангенсу угла наклона (tg a). Если значения Хпред, определенные для всех температур, изменяются
незакономерно и отличаются друг от друга не более, чем на величину максимальной
относительной ошибки среднего арифметического значения показателя, то вычисляют
значение
, как показано на черт. 2, и
определяют Хпред по отрезку, отсекаемому этой
прямой на оси абсцисс; константу К
- по тангенсу угла наклона (tg a). Если значения Хпред, определенные для всех температур, изменяются
незакономерно и отличаются друг от друга не более, чем на величину максимальной
относительной ошибки среднего арифметического значения показателя, то вычисляют
значение ![]() по формуле
по формуле
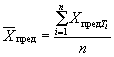 ,
,
где ![]() - предельное значение
показателя при Тi;
- предельное значение
показателя при Тi;
п - число температур старения.
Если
определение Хпред возможно только при Тп-1
и Тn, то
вычисляют среднее
значение ![]() по формуле
по формуле
![]() .
.
1.5. Если Хпред определено
по результатам испытания при всех температурах, то обработку по пп. 1.1 - 1.3 не
проводят. Вычисляют ![]() по п. 1.4.
по п. 1.4.
Строят
график зависимости ![]() от t, как
показано на черт. 3.
от t, как
показано на черт. 3.
Черт. 3
Черт. 4
Константу К определяют по тангенсу угла наклона графика к оси абсцисс (K = tga).
1.6. По значениям констант K, определенным при каждой температуре старения,
строят график зависимости lnК от ![]() , как показано на черт. 4.
, как показано на черт. 4.
1.7. Определяют тангенс угла наклона графика к оси абсцисс (tga) и вычисляют коэффициент Е по формуле
![]() .
.
1.8. Экстраполируют график зависимости lnК от ![]() на
эквивалентную температуру Тэ, установленную
по коэффициенту Е, вычисленному по п. 1.6, для
заданных условий хранения в соответствии с обязательным приложением 5 и
определяют значение константы скорости процесса
на
эквивалентную температуру Тэ, установленную
по коэффициенту Е, вычисленному по п. 1.6, для
заданных условий хранения в соответствии с обязательным приложением 5 и
определяют значение константы скорости процесса ![]() при Тэ,
как показано на черт. 4.
при Тэ,
как показано на черт. 4.
1.9. Подставляя полученные значения ![]() и
и ![]() в уравнение (1),
вычисляют значения Xi для заданных значений ti. Строят график зависимости Xi от
в уравнение (1),
вычисляют значения Xi для заданных значений ti. Строят график зависимости Xi от ![]() (кривую прогноза).
(кривую прогноза).
2. Если не выполняются условия п. 1.3, то кинетические кривые зависимости X от t описывают уравнением h-гo порядка типа
где
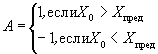
(Измененная редакция, Изм. № 1).
2.1. Обработку проводят в соответствии с требованиями пп. 1.1 - 1.2.
2.2. Строят
график зависимости ![]() от Х для
каждой из температур, экстраполируя
последний линейный участок каждого из графиков на значение
от Х для
каждой из температур, экстраполируя
последний линейный участок каждого из графиков на значение ![]() = 0 находят
= 0 находят ![]() как показано на черт.
5.
Определяют значение
как показано на черт.
5.
Определяют значение ![]() в соответствии с п.
1.4.
в соответствии с п.
1.4.
Черт. 5
Черт. 6
2.3.
Строят график зависимости ln![]() от ln
от ln![]() , как показано на черт. 6. Константу К определяют
по отрезку, отсекаемому на оси ординат, а значение h - по
тангенсу угла наклона графика к оси абсцисс.
, как показано на черт. 6. Константу К определяют
по отрезку, отсекаемому на оси ординат, а значение h - по
тангенсу угла наклона графика к оси абсцисс.
Линейность графика и независимость h от температуры являются критериями правомерности применения уравнения (2).
(Измененная редакция, Изм. № 1).
2.4. Прогнозирование изменения показателя проводят с применением уравнения (2) в соответствии с требованиями пп. 1.6 - 1.10.
3. Обработка результатов испытаний для обратимых процессов первого порядка в случае, если предельное значение показателя Хпред зависит от температуры, как показано на черт. 7.
3.1.
Описывают кинетические кривые зависимости Х от t
уравнением (1)
при К = К1 + К2 и Хпред
= ![]() , где K1 и K2 -
соответственно константы
скоростей прямой и обратной стадий процесса, Х0 -
исходное значение показателя.
, где K1 и K2 -
соответственно константы
скоростей прямой и обратной стадий процесса, Х0 -
исходное значение показателя.
(Измененная редакция, Изм. № 1).
3.2. Значения К и Хпред устанавливают в соответствии с пп. 1.1 - 1.5. По значениям Хпред и К вычисляют значения K1 и K2 для каждой температуры испытаний по формулам:
![]() ,
,
![]() .
.
Признаком
обратимых процессов при монотонном изменении показателя являются линейность
графиков зависимости ![]() от Х и зависимость Хпред от температуры.
от Х и зависимость Хпред от температуры.
3.3. По
вычисленным для каждой температуры значениям K1 и K2 строят графики зависимости lnK1 от ![]() и lnK2 от
и lnK2 от ![]() , как показано на черт. 8.
, как показано на черт. 8.
Черт. 7
Черт. 8
3.4. Определив тангенсы углов наклона графиков к оси абсцисс, вычисляют коэффициенты Е1 и Е2 соответственно для прямой и обратной стадий процесса по формулам:
![]() ,
,
![]()
3.5. По вычисленным значениям Е1 и Е2 и обязательному приложению 5 определяют эквивалентные температуры Тэ1 и Тэ2 для заданных условий хранения.
3.6.
Экстраполируют графики зависимости lnK1 от ![]() и lnK2 от
и lnK2 от ![]() соответственно на Тэ1
и Тэ2, определяют
соответственно на Тэ1
и Тэ2, определяют ![]() и
и ![]() , как показано на черт. 8, и вычисляют
, как показано на черт. 8, и вычисляют ![]() и
и ![]() .
.
3.7.
Определяют ![]() и Xпред по
формулам:
и Xпред по
формулам:
![]() ,
,
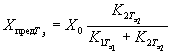 .
.
Используя уравнение (1) в соответствии с требованиями пп. 1.9 - 1.10, строят кривую прогноза и проводят прогнозирование.
4. Обработка результатов испытаний в случае двух неконкурирующих процессов первого порядка.
4.1. По результатам испытаний, полученным по методу 1 настоящего стандарта, в соответствии с требованиями п. 1.1, для каждой температуры испытаний строят кинетические кривые зависимости изменения показателя от продолжительности старения, как показано на черт. 9.
Черт. 9
4.2. Кинетические кривые описывают уравнением первого порядка типа
![]() . (3)
. (3)
Знаки при коэффициентах g1 и g2 должны совпадать.
4.3.
Значение Xпред
определяют в соответствии с требованиями п. 2.2. Значение ![]() определяют в
соответствии с требованиями п. 1.4.
определяют в
соответствии с требованиями п. 1.4.
Черт. 10
Черт. 11
4.4.
Строят графики зависимости ![]() от t, если Х(t) <
от t, если Х(t) < ![]() , как показано на черт. 10, или
, как показано на черт. 10, или ![]() от t, если Х(t) >
от t, если Х(t) > ![]() , как показано на черт. 11; экстраполируют конечный
линейный участок графика на оси ординат и находят lng1, как отрезок, отсекаемый на этой
оси. Константу К1 определяют по тангенсу угла наклона
линейного участка к оси абсцисс.
, как показано на черт. 11; экстраполируют конечный
линейный участок графика на оси ординат и находят lng1, как отрезок, отсекаемый на этой
оси. Константу К1 определяют по тангенсу угла наклона
линейного участка к оси абсцисс.
4.5. Для каждой температуры вычисляют вспомогательные функции
![]() , если
, если ![]() ,
,
![]() , если
, если ![]() .
.
4.6. Строят график зависимости lnZ от t, как показано на черт. 12, и определяют lng2, по отрезку, отсекаемому на оси ординат, а К2 - по тангенсу угла наклона графика к оси абсцисс.
4.7. В том случае, когда Х0 определено как среднее арифметическое значение по результатам испытаний не менее тридцати образцов, значение g2 вычисляют по уравнениям:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Вычисляют вспомогательные функции
![]() , если
, если ![]()
или ![]() , если
, если ![]() .
.
Строят график зависимости lnz(t) от t и определяют константу K2 по тангенсу угла наклона графика к оси абсцисс.
Черт. 12
Черт. 13
4.8. Строят графики зависимостей lnK1 от ![]() и lnK2 от
и lnK2 от ![]() , как показано на черт. 13.
Определяют тангенсы углов наклона этих графиков к оси абсцисс и вычисляют
коэффициенты E1 и Е2 по формулам:
, как показано на черт. 13.
Определяют тангенсы углов наклона этих графиков к оси абсцисс и вычисляют
коэффициенты E1 и Е2 по формулам:
![]() ,
,
![]() .
.
4.9. По
значениям E1 и Е2
и обязательному приложению 5 для заданных условий хранения определяют Тэ1
и Тэ2. Экстраполируют графики, приведенные на черт. 13, на
температуры Тэ1 и Тэ2 и определяют ![]() и
и ![]() по значениям
по значениям ![]() и
и ![]() .
.
4.10. Если коэффициенты g1 и g2 незакономерно изменяются от температуры, то
вычисляют средние значения ![]() и
и ![]() .
.
В случае закономерного изменения gi от температуры зависимость gi от Т описывают обратным полиномом второй степени в соответствии с рекомендуемым приложением 6, заменяя параметр X на gI, а параметр t на T и определяют значения g1 и g2 при эквивалентных температурах Тэ1 и Тэ2.
4.11.
Используя полученные значения ![]() , g1, g2,
, g1, g2, ![]() ,
, ![]() и уравнение (3),
строят кривую прогноза и проводят прогнозирование в соответствии с требованиями
пп. 1.9
- 1.10.
и уравнение (3),
строят кривую прогноза и проводят прогнозирование в соответствии с требованиями
пп. 1.9
- 1.10.
5. Способ обработки результатов испытаний при получении кинетических кривых, имеющих экстремумы.
5.1. По результатам испытаний, полученным по методу 1 настоящего стандарта, в соответствии с требованиями п. 1.1 строят кинетические кривые.
5.2. Описывают кинетические кривые уравнением первого порядка типа
![]() , (4)
, (4)
где g1 и g2 - коэффициенты;
К1 и K2 - константы скоростей процессов.
5.3.
Значение Хпред определяют в соответствии с требованиями п. 2.2.
Значение ![]() определяют по п. 1.4.
определяют по п. 1.4.
5.4. При наличии максимума на кинетических кривых, как
показано на черт. 14, строят график зависимости ![]() от t, как
показано на черт. 15, при t > tm, и по линейному участку графика определяют lng1 по отрезку, отсекаемому на оси ординат, a K1 - по тангенсу угла наклона графика к оси абсцисс.
от t, как
показано на черт. 15, при t > tm, и по линейному участку графика определяют lng1 по отрезку, отсекаемому на оси ординат, a K1 - по тангенсу угла наклона графика к оси абсцисс.
Черт. 14
Черт. 15
5.4.1. Вычисляют вспомогательную функцию
![]()
в диапазоне испытаний от t = 0 до tm для каждой температуры.
5.4.2. Строят график зависимости lnZ(t) от t, как показано на черт. 16, и по отрезку, отсекаемому прямой на оси ординат, определяют lng2, а по тангенсу угла наклона прямой к оси абсцисс - константу К2.
5.5. При наличии минимума на кинетических кривых, как
показано на черт. 17, строят график зависимости ![]() от t, при t > tm. Экстраполируют линейный участок графика на ось ординат и определяют lng2 по отрезку, отсекаемому на этой оси. Константу К2
определяют по тангенсу угла наклона линейного участка к оси абсцисс.
от t, при t > tm. Экстраполируют линейный участок графика на ось ординат и определяют lng2 по отрезку, отсекаемому на этой оси. Константу К2
определяют по тангенсу угла наклона линейного участка к оси абсцисс.
5.5.1. Вычисляют вспомогательную функцию
![]()
в диапазоне испытаний от t = 0 до tm.
5.5.2. Строят график зависимости lnZ(t) от t.
По отрезку, отсекаемому прямой на оси ординат, определяют lng1; по тангенсу угла наклона прямой к оси абсцисс - К1.
5.6. Если Х0 определено как среднее арифметическое значение по результатам испытаний не менее тридцати образцов, то при наличии максимума на кривых значения g1 и К1 определяют в соответствии с требованиями п. 5.4; значение g2 вычисляют при t = 0 по уравнению
![]() , (5)
, (5)
значение К2 -
по тангенсу угла наклона графика зависимости lnZ(t) от t к оси абсцисс, где ![]() .
.
Черт. 16
Черт. 17
При наличии минимума на кривых значения g2 и К2 определяют в соответствии с требованиями п. 5.5.
Значение g1
определяют по уравнению (5) при t = 0. Значение К1 - определяют по
тангенсу угла наклона графика зависимости lnZ(t) от t к оси абсцисс, где ![]() .
.
5.7.
Определяют ![]()
![]() ,g1 и g2 при Тэ1 и
Тэ2 в соответствии с требованиями пп. 4.8 - 4.10 и
используя уравнение (4), строят кривую прогноза и проводят
прогнозирование в соответствии с требованиями пп. 1.9 - 1.10.
,g1 и g2 при Тэ1 и
Тэ2 в соответствии с требованиями пп. 4.8 - 4.10 и
используя уравнение (4), строят кривую прогноза и проводят
прогнозирование в соответствии с требованиями пп. 1.9 - 1.10.
6. Обработка результатов испытаний, если зависимости X от t представляют собой S-образные кинетические кривые.
S-образные кинетические кривые описывают уравнением Колмогорова - Ерофеева или уравнением автокаталитических процессов.
6.1. Обработка результатов испытаний с применением уравнения Колмогорова - Ерофеева вида
![]() . (6)
. (6)
6.1.1. По результатам испытаний, полученным по методу 1 настоящего стандарта, строят кинетические кривые, как показано на черт. 18.
6.1.2.
Значение ![]() определяют в
соответствии с требованиями пп. 1.1 - 1.5.
определяют в
соответствии с требованиями пп. 1.1 - 1.5.
6.1.3.
Строят график зависимости ![]() от lnt.
от lnt.
При правомерности описания кинетических кривых уравнением (6) экспериментальные точки в указанных координатах должны укладываться на прямую, как показано на черт. 19.
6.1.4. Значения lnК для каждой из температур испытаний определяют по отрезку, отсекаемому графиком на оси ординат, как показано на черт. 19, а коэффициент l - по тангенсу угла наклона прямой к оси абсцисс.
6.1.5. Если значения коэффициента li незакономерно изменяются при различных Тi, то вычисляют lср по формуле
![]() ,
,
где п - число температур испытаний.
Для
определения значения ![]() проводят
обработку в соответствии с требованиями пп. 1.6 - 1.8.
проводят
обработку в соответствии с требованиями пп. 1.6 - 1.8.
6.1.6.
Используя значения ![]() ,
, ![]() и lср
описывают кривую прогноза
уравнением (6) и проводят прогнозирование в соответствии с
требованиями пп. 1.9 - 1.10.
и lср
описывают кривую прогноза
уравнением (6) и проводят прогнозирование в соответствии с
требованиями пп. 1.9 - 1.10.
Черт. 18
Черт. 19
6.1.7. Установление закономерной зависимости l от Т является критерием неправомерности применения уравнения (6).
(Измененная редакция, Изм. № 1).
6.2 - 6.2.7. (Исключены, Изм. № 1).
7. Обработка результатов испытаний экспоненциальным полиномом.
7.1. В случае, если ни одно из приведенных в разд. 1 - 6 уравнений не пригодно для описания результатов испытаний, то их обработку проводят с помощью экспоненциального полинома вида
![]() . (8)
. (8)
7.2. Значение Хпред для каждой температуры определяют в соответствии с п. 2.2.
7.3.
Значение ![]() находят в
соответствии с п. 1.4.
находят в
соответствии с п. 1.4.
7.4. Для каждой температуры испытаний вычисляют вспомогательные функции
![]()
в соответствии с требованиями, изложенными ниже.
7.4.1. Вычисляют вспомогательную функцию ![]() для каждой температуры. Строят график зависимости
для каждой температуры. Строят график зависимости ![]() от t.
Экстраполируя линейный участок графика на ось ординат, определяют
от t.
Экстраполируя линейный участок графика на ось ординат, определяют ![]() , как отрезок, отсекаемый на этой оси; константу К1
определяют по тангенсу угла наклона линейного участка графика к оси
абсцисс.
, как отрезок, отсекаемый на этой оси; константу К1
определяют по тангенсу угла наклона линейного участка графика к оси
абсцисс.
7.4.2. Вычисляют вспомогательную функцию
![]()
и строят график зависимости ![]() от t.
от t.
Константу
K2 и ![]() определяют как
указано в п. 7.4.1.
определяют как
указано в п. 7.4.1.
7.4.3.
Вычисления функции Zn(t) повторяют до получения линейной зависимости ![]() от t при всех
значениях t. Знак
от t при всех
значениях t. Знак ![]() выбирают из
условия соответствия знаку функции
выбирают из
условия соответствия знаку функции ![]() .
.
7.5. Строят графики зависимостей lnКi от ![]() . Определив тангенсы углов наклонов трафиков к оси
абсцисс, вычисляют коэффициенты Еi по формуле:
. Определив тангенсы углов наклонов трафиков к оси
абсцисс, вычисляют коэффициенты Еi по формуле:
![]() .
.
7.6. По
значению Еi для заданных условий хранения определяют температуры
![]() в соответствии
с требованиями обязательного приложения 5.
в соответствии
с требованиями обязательного приложения 5.
7.7.
Экстраполируют графики, полученные по п. 7.5, на температуры ![]() и определяют
и определяют ![]() для каждой
стадии процесса.
для каждой
стадии процесса.
7.8.
Значения ![]() уточняют в
соответствии с требованиями п. 4.10.
уточняют в
соответствии с требованиями п. 4.10.
7.9. Используя значения ![]() ;
; ![]() ,
, ![]() , описывают кривую прогноза уравнением (8) и
проводят прогнозирование в соответствии с пп. 1.9 - 1.10.
, описывают кривую прогноза уравнением (8) и
проводят прогнозирование в соответствии с пп. 1.9 - 1.10.
8. Алгоритм обработки на ЭВМ результатов испытаний по методу 1
При выборе кинетического уравнения для аппроксимации результатов ускоренных испытаний по методу 1 необходимо исходить из знаний о физико-химической природе исследуемого полимерного материала и вида лекальных кривых, построенных по результатам испытаний.
8.1. Экспериментальные данные изменения показателя от
продолжительности старения при каждой температуре испытаний описывают обратным
полиномом второй степени в соответствии с приложением 6. При этом
общий средний исходный показатель для всех температур ![]() вычисляют по
формуле
вычисляют по
формуле
где a0i, a1i, a2i - коэффициенты обратных полиномов 2-й степени для i-й температуры испытаний.
8.2.
Зависимость изменения рассчитанных по п. 8.1 значений показателя ![]() от продолжительности
испытаний при каждой температуре описывают кинетическим уравнением 1-го порядка вида
от продолжительности
испытаний при каждой температуре описывают кинетическим уравнением 1-го порядка вида
где ![]() ,
, ![]() - соответственно
исходное и предельное средние значения показателя;
- соответственно
исходное и предельное средние значения показателя;
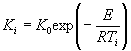 - константа
скорости процесса;
- константа
скорости процесса;
К0 - предэкспонента;
i - порядковый номер температуры испытаний, i = l, 2, 3, ..., п;
п - число температур испытаний;
j - порядковый номер съема, j = 1, 2, 3, ..., mi, где тi - число съемов при каждой температуре испытаний.
8.2.1.
Уравнение (2)
для ![]() = 0
приводится к виду
= 0
приводится к виду
8.2.2. Если ![]() не достигается в
процессе испытаний при всех температурах, вычисляют производные обратного
полинома второй степени, использованного по п. 8.1 для
каждой температуры, по формуле
не достигается в
процессе испытаний при всех температурах, вычисляют производные обратного
полинома второй степени, использованного по п. 8.1 для
каждой температуры, по формуле
где a1i и a2i - коэффициенты уравнений, полученные по п. 8.1.
8.2.3.
Зависимость ![]() от
от ![]() описывают линейным
уравнением вида
описывают линейным
уравнением вида
8.2.4. Коэффициенты уравнения (5) вычисляют методом наименьших квадратов
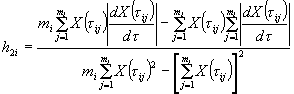 . (7)
. (7)
8.2.5. Параметры уравнения (2) ![]() и Кi для каждой из температур определяют из соотношений:
и Кi для каждой из температур определяют из соотношений:
![]() . (9)
. (9)
8.2.6. Вычисляют среднее значение ![]() для всех температур
по формуле
для всех температур
по формуле
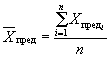 , (10)
, (10)
где ![]() - предельный
показатель при каждой из температур испытаний Тi;
- предельный
показатель при каждой из температур испытаний Тi;
п - число температур испытаний.
Если
вычисленное значение ![]() меньше 5 % исходного
меньше 5 % исходного ![]() значения
показателя,
значения
показателя, ![]() принимают (считают)
равным нулю.
принимают (считают)
равным нулю.
8.2.7.
Зависимость lnКi от ![]() для каждой
температуры описывают линейным уравнением вида
для каждой
температуры описывают линейным уравнением вида
8.2.8. Коэффициенты уравнения (11) вычисляют методом наименьших квадратов:
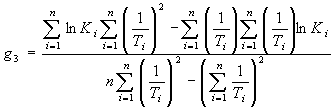 ; (12)
; (12)
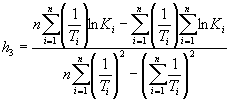 . (13)
. (13)
8.2.9. Коэффициент температурной зависимости процесса Е и предэкспоненту К0 уравнения 2 вычисляют по соотношениям:
E = R×h3; (14)
K0 = expg3. (15)
8.2.10.
Рассчитывают показатель ![]() по уравнению (2),
используя полученные
параметры
по уравнению (2),
используя полученные
параметры ![]() и
и 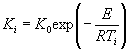 .
.
8.2.11. Среднюю квадратичную ошибку аппроксимации (D1) экспериментальных данных уравнением (2) при всех температурах вычисляют по формуле
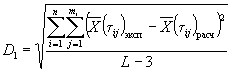 , (16)
, (16)
где ![]() - общее число съемов
при всех температурах.
- общее число съемов
при всех температурах.
8.3.
Зависимость изменения показателя ![]() от
продолжительности испытаний при каждой из температур, обработанная обратным
полиномом 2-й степени по п. 8.1, описывают кинетическим уравнением (2) при
от
продолжительности испытаний при каждой из температур, обработанная обратным
полиномом 2-й степени по п. 8.1, описывают кинетическим уравнением (2) при ![]() ,
, ![]() , где K1i и K2i - константы скоростей прямой и
обратной стадий процесса соответственно. При этом уравнение (2)
принимает вид
, где K1i и K2i - константы скоростей прямой и
обратной стадий процесса соответственно. При этом уравнение (2)
принимает вид
8.3.1. Значения Ki и ![]() для каждой из температур устанавливают в соответствии с пп. 8.2.2 - 8.2.5.
для каждой из температур устанавливают в соответствии с пп. 8.2.2 - 8.2.5.
8.3.2. Вычисляют K1i и K2i для каждой из температур по соотношениям:
![]() ; (18)
; (18)
![]() . (19)
. (19)
8.3.3.
Зависимость lnК1i и lnК2i от ![]() описывают линейным
уравнением вида
описывают линейным
уравнением вида
8.3.4. Коэффициенты h4, h5, g4 и g5 уравнений (20 и 21) вычисляют методом наименьших квадратов по формулам:
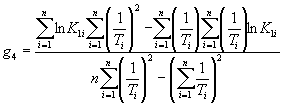 ; (22)
; (22)
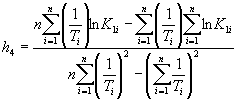 ; (23)
; (23)
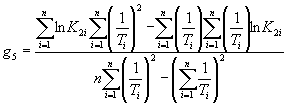 ; (24)
; (24)
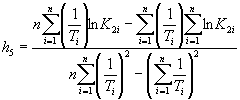 . (25)
. (25)
8.3.5. Коэффициенты температурной зависимости прямой и обратной стадий процесса E1 и E2, а также предэкспоненты К01 и К02 определяют из соотношений:
E1 = R×h4; (26)
E2 = R×h5; (27)
K01 = expg4; (28)
K02 = expg5. (29)
8.3.6.
Значения ![]() ;
; 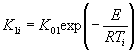 и
и 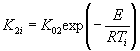 , определенные
для каждой температуры по п. 8.3.1, подставляют в уравнение (17) и
вычисляют
, определенные
для каждой температуры по п. 8.3.1, подставляют в уравнение (17) и
вычисляют ![]() для каждого съема при
каждой температуре.
для каждого съема при
каждой температуре.
8.3.7. Среднюю квадратичную ошибку аппроксимации результатов испытаний уравнением (17) при всех температурах вычисляют по формуле
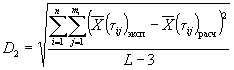 ; (30)
; (30)
8.4.
Зависимость изменения показателя ![]() от продолжительности
испытаний при каждой из температур, обработанная по п. 8.1, описывают уравнением h -
порядка вида
от продолжительности
испытаний при каждой из температур, обработанная по п. 8.1, описывают уравнением h -
порядка вида
Если ![]() , то в формуле (31) перед скобкой ставят знак «-», если
, то в формуле (31) перед скобкой ставят знак «-», если ![]() , то перед скобкой ставят знак «+».
, то перед скобкой ставят знак «+».
8.4.1. Вычисляют предельное значение показателя ![]() для каждой
температуры с использованием уравнения обратного полинома 2-й степени в соответствии
с приложением 6 из соотношения
для каждой
температуры с использованием уравнения обратного полинома 2-й степени в соответствии
с приложением 6 из соотношения
![]() , (32)
, (32)
где ![]() - коэффициенты
обратного полинома 2-й степени для каждой из температур по п. 8.1.
- коэффициенты
обратного полинома 2-й степени для каждой из температур по п. 8.1.
8.4.2. Вычисляют среднее значение ![]() по формуле
по формуле
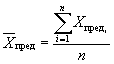 . (33)
. (33)
8.4.3.
Зависимость ![]() от
от ![]() для каждой из
температур описывают линейным уравнением вида:
для каждой из
температур описывают линейным уравнением вида:
8.4.4. Коэффициенты уравнения (34) вычисляют методом наименьших квадратов по формулам:
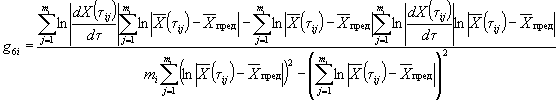 ; (35)
; (35)
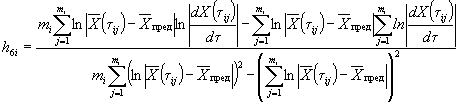 . (36)
. (36)
8.4.5. Параметры уравнения (31) Ki и hi при каждой из температур определяют из соотношений:
![]() ; (37)
; (37)
![]() . (38)
. (38)
8.4.6. Среднее значение параметра h определяют по формуле
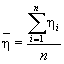 . (39)
. (39)
8.4.7.
Зависимость lnКi от ![]() описывают линейным
уравнением вида:
описывают линейным
уравнением вида:
8.4.8. Коэффициенты уравнения (40) вычисляют методом наименьших квадратов по формулам:
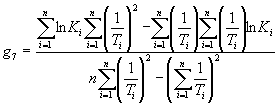 ; (41)
; (41)
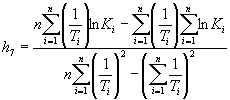 . (42)
. (42)
8.4.9. Коэффициент Е процесса и предэкспоненту К0 определяют из соотношений:
E = R×h7; (43)
K0 = expg7. (44)
8.4.10.
Вычисляют показатель ![]() по уравнению 31,
используя полученные параметры
по уравнению 31,
используя полученные параметры ![]() ,
, ![]() ,
, ![]() и
и ![]()
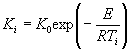 .
.
8.4.11. Среднюю квадратичную ошибку аппроксимации результатов испытаний уравнением (31) при всех температурах вычисляют по формуле
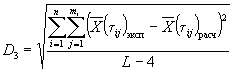 . (45)
. (45)
8.5.
Зависимости изменения показателей ![]() расч от продолжительности испытаний при каждой из
температур, обработанные по п. 8.1, описывают кинетическим уравнением вида:
расч от продолжительности испытаний при каждой из
температур, обработанные по п. 8.1, описывают кинетическим уравнением вида:
Знаки при
коэффициентах ![]() и
и ![]() должны совпадать.
Если
должны совпадать.
Если ![]() , ставят знак «+»,
, ставят знак «+»,![]() - знак «-».
- знак «-».
8.5.1.
Предельные значения показателей для каждой из температур ![]() определяют в
соответствии с п. 8.4.1, а среднее значение
определяют в
соответствии с п. 8.4.1, а среднее значение ![]() - в соответствии
с п. 8.4.2.
- в соответствии
с п. 8.4.2.
8.5.2. Вычисляют производную 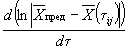 для
продолжительности испытаний tmi, соответствующей последнему съему при каждой из
температур по формуле
для
продолжительности испытаний tmi, соответствующей последнему съему при каждой из
температур по формуле
где а0i, а1i, а2i - коэффициенты обратных полиномов 2-й степени по п. 8.1.
8.5.3. Вычисляют коэффициенты К1i и g1i уравнения (47) для каждой из температур испытаний по формулам:
![]() ; (48)
; (48)
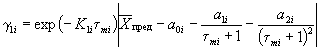 , (49)
, (49)
где а0i, а1i, а2i - по п. 8.5.2.
8.5.4. Для каждой температуры испытаний вычисляют вспомогательную функцию Z(tij) по формуле
![]() . (50)
. (50)
8.5.5.
Зависимость ![]() от продолжительности
испытаний tij, при
каждой температуре описывают линейным уравнением вида:
от продолжительности
испытаний tij, при
каждой температуре описывают линейным уравнением вида:
8.5.6. Коэффициенты уравнения (51) рассчитывают методом наименьших квадратов по формулам:
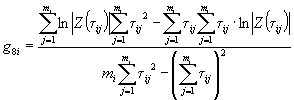 ; (52)
; (52)
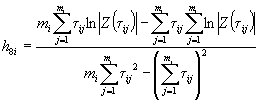 . (53)
. (53)
8.5.7. Параметры К2i и g2i уравнения (46) определяют из соотношений:
![]() ; (54)
; (54)
![]() . (55)
. (55)
8.5.8.
Средние значения ![]() и
и ![]() вычисляют по
формулам:
вычисляют по
формулам:
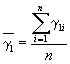 ; (56)
; (56)
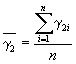 . (57)
. (57)
8.5.9.
Зависимости lnК1i и lnК2i от ![]() описывают линейными
уравнениями вида:
описывают линейными
уравнениями вида:
8.5.10. Коэффициенты уравнений (58) и (59) g9; g10; h9; h10 рассчитывают методом наименьших квадратов по формулам:
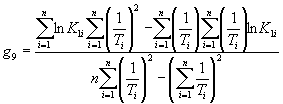 ; (60)
; (60)
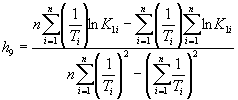 ; (61)
; (61)
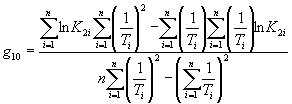 ; (62)
; (62)
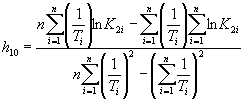 . (63)
. (63)
8.5.11. Коэффициенты Е1 и Е2, а также предэкспоненты K01 и K02 находят из соотношений:
E1 = R×h9; (64)
E2 = R×h10; (65)
K01 = expg9; (66)
K02 = expg10. (67)
8.5.12.
Вычисляют ![]() по формуле (46),
используя значения параметров:
по формуле (46),
используя значения параметров:
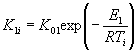 ;
; 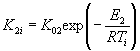 ;
; ![]() ;
; ![]() ;
; ![]() .
.
8.5.13. Среднюю квадратичную ошибку аппроксимации результатов испытаний уравнением (46) при всех температурах вычисляют по формуле
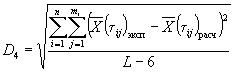 . (68)
. (68)
8.6. Экспериментальные данные по изменению показателя ![]() от
продолжительности испытаний
от
продолжительности испытаний ![]() при каждой из
температур группируют в две совокупности: 1 - от исходного показателя до его
значения при съеме тi/2; 2 - от значения в съеме (тi/2 + 1) до значения в последнем съеме mi.
при каждой из
температур группируют в две совокупности: 1 - от исходного показателя до его
значения при съеме тi/2; 2 - от значения в съеме (тi/2 + 1) до значения в последнем съеме mi.
Каждую из этих совокупностей описывают обратным полиномом 2-й степени в соответствии с приложением 6.
Продолжительность испытаний, при которой обе совокупности имеют одинаковое значение показателя, вычисляют по формуле
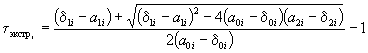 , (69)
, (69)
где а0i, а1i, а2i - коэффициенты обратных полиномов, описывающих первую совокупность при каждой из температур;
d0i, d1i, d2i - коэффициенты обратных полиномов 2-й степени, описывающих вторую совокупность при каждой из температур;
![]() - определяют по формуле 1, используя коэффициенты а0i, а1i, а2i.
- определяют по формуле 1, используя коэффициенты а0i, а1i, а2i.
8.6.1. Зависимости изменения показателя от продолжительности испытаний при каждой из температур, обработанные по п. 8.6, только при tэкстр > 0, описывают кинетическим уравнением вида:
8.6.2.
Предельное значение показателя ![]() при каждой
температуре с использованием обратного полинома 2-й степени для совокупности 2
в соответствии с приложением 6 вычисляют по формуле
при каждой
температуре с использованием обратного полинома 2-й степени для совокупности 2
в соответствии с приложением 6 вычисляют по формуле
![]() . (71)
. (71)
8.6.3.
Среднее значение ![]() определяют в
соответствии с п. 8.2.6.
определяют в
соответствии с п. 8.2.6.
8.6.4.
Значение показателя в точке экстремума ![]() вычисляют по формуле
вычисляют по формуле
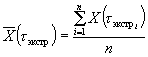 ,
,
где ![]() . (72)
. (72)
8.6.5.
Производную 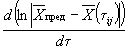 для совокупности 2 при продолжительности испытаний
для совокупности 2 при продолжительности испытаний ![]() , соответствующей последнему съему при каждой из температур,
вычисляют по формуле
, соответствующей последнему съему при каждой из температур,
вычисляют по формуле
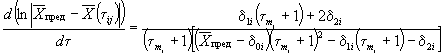 . (73)
. (73)
8.6.6. Параметры g1i и K1i при ![]() для каждой из
температур вычисляют по формулам:
для каждой из
температур вычисляют по формулам:
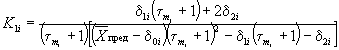 ; (74)
; (74)
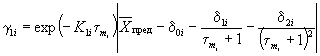 . (75)
. (75)
8.6.7. Для каждой температуры испытаний в совокупности 1, вспомогательную функцию Z(tij) в интервале от t = 0 до t = tэкстр (точка экстремума) вычисляют по формуле
![]() . (76)
. (76)
8.6.8. Зависимость lnZ(tij) от продолжительности испытаний tij при каждой температуре для совокупности 1 описывают линейным уравнением вида:
Коэффициенты уравнения (77) вычисляют методом наименьших квадратов по формулам:
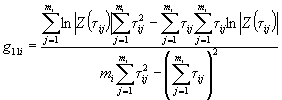 ; (78)
; (78)
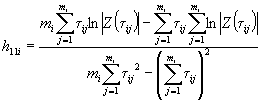 . (79)
. (79)
8.6.9. Параметры К2i и g2i уравнения 70 для каждой температуры определяют из соотношений:
![]() ; (80)
; (80)
![]() . (81)
. (81)
8.6.10. Параметры g2i и К2i при ![]() для каждой из
температур для совокупности 2 вычисляют по формулам:
для каждой из
температур для совокупности 2 вычисляют по формулам:
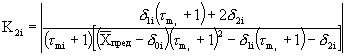 ; (82)
; (82)
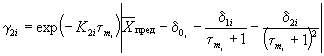 . (83)
. (83)
8.6.11. Для каждой из температур испытаний в совокупности 1 вычисляют вспомогательную функцию Z(tij)1 в интервале от t = 0 до t = tэкстр по формуле
![]() . (84)
. (84)
8.6.12.
Зависимость ![]() от
продолжительности испытаний при каждой температуре описывают линейным
уравнением вида:
от
продолжительности испытаний при каждой температуре описывают линейным
уравнением вида:
Коэффициенты уравнения (85) (g12i и h12i) рассчитывают методом наименьших квадратов по формулам:
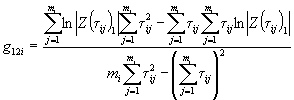 ; (86)
; (86)
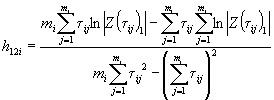 . (87)
. (87)
8.6.13. Значения параметров К1i и g1i уравнения (70) для каждой температуры определяют из соотношений:
![]() ; (88)
; (88)
![]() . (89)
. (89)
8.6.14.
Зависимости lnК1i и lnК2i от ![]() описывают линейными
уравнениями вида:
описывают линейными
уравнениями вида:
При этом,
если ![]() , то значения К1i и К2i устанавливают по пп. 8.6.6 и
8.6.9,
а если
, то значения К1i и К2i устанавливают по пп. 8.6.6 и
8.6.9,
а если ![]() , то значения К1i и К2i устанавливают по пп. 8.6.10
и 8.6.13.
, то значения К1i и К2i устанавливают по пп. 8.6.10
и 8.6.13.
Коэффициенты уравнений (90 и 91) вычисляют методом наименьших квадратов по формулам:
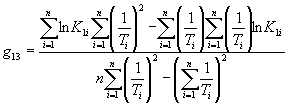 ; (92)
; (92)
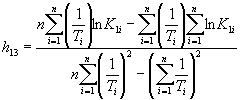 ; (93)
; (93)
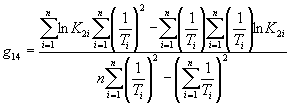 ; (94)
; (94)
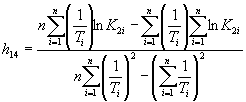 . (95)
. (95)
8.6.15. Коэффициенты температурной зависимости Е1 и Е2, а также предэкспоненты K01 и К02 вычисляют из соотношений:
E1 = R×h13; (96)
E2 = R×h14; (97)
K01 = expg13; (98)
K02 = expg14. (99)
8.6.16.
Средние значения ![]() и
и ![]() вычисляют по
формулам:
вычисляют по
формулам:
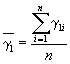 ; (100)
; (100)
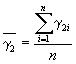 . (101)
. (101)
При этом,
если ![]() , то значения g1i и g2i устанавливают из пп. 8.6.6 и 8.6.9;
а если
, то значения g1i и g2i устанавливают из пп. 8.6.6 и 8.6.9;
а если ![]() - то по пп. 8.6.10
и 8.6.13.
- то по пп. 8.6.10
и 8.6.13.
8.6.17.
Рассчитывают значения показателя ![]() по уравнению (70),
используя полученные параметры:
по уравнению (70),
используя полученные параметры:
![]() ;
; ![]() ;
; ![]() ;
; 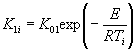 ;
; 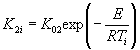 .
.
8.6.18. Среднюю квадратическую ошибку аппроксимации экспериментальных данных уравнением (70) при всех температурах ускоренных испытаний вычисляют по формуле
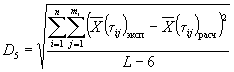 . (102)
. (102)
8.7. Экспериментальные данные по изменению показателя ![]() от продолжительности
испытаний при каждой из температур, начиная со значения
от продолжительности
испытаний при каждой из температур, начиная со значения ![]() , соответствующего съему (mi/2 + 1), до значения показателя, соответствующего
съему mi, обрабатывают по п. 8.1.
, соответствующего съему (mi/2 + 1), до значения показателя, соответствующего
съему mi, обрабатывают по п. 8.1.
8.7.1. Предельные значения показателя ![]() для каждой
температуры по уравнению обратного полинома 2-й степени в соответствии с
приложением 6 для экспериментальных точек, начиная с(mi/2 + 1) до mi, вычисляют по формуле
для каждой
температуры по уравнению обратного полинома 2-й степени в соответствии с
приложением 6 для экспериментальных точек, начиная с(mi/2 + 1) до mi, вычисляют по формуле
![]() . (103)
. (103)
Среднее
значение ![]() вычисляют по п. 8.2.6.
вычисляют по п. 8.2.6.
8.7.2.
Зависимости ![]() от tij полученные экспериментально,
описывают кинетическим уравнением вида:
от tij полученные экспериментально,
описывают кинетическим уравнением вида:
8.7.3.
Зависимость 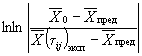 от продолжительности
испытаний (tij) при
каждой температуре и при всех съемах описывают линейным уравнением вида:
от продолжительности
испытаний (tij) при
каждой температуре и при всех съемах описывают линейным уравнением вида:
Коэффициенты уравнения (105) вычисляют методом наименьших квадратов по формулам:
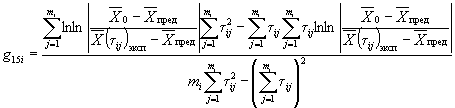 ; (106)
; (106)
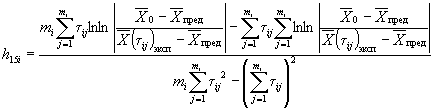 . (107)
. (107)
8.7.4. Значения параметров Ki и li уравнения (104) определяют из соотношений:
![]() ; (108)
; (108)
![]() . (109)
. (109)
8.7.5.
Среднее значение ![]() вычисляют по формуле
вычисляют по формуле
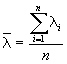 . (110)
. (110)
8.7.6. Зависимость lnКi от ![]() описывают линейными
уравнениями вида:
описывают линейными
уравнениями вида:
Коэффициенты уравнения (111) рассчитывают методом наименьших квадратов по формулам:
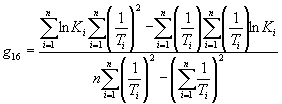 ; (112)
; (112)
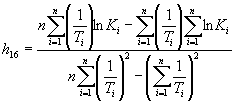 . (113)
. (113)
8.7.7. Коэффициент температурной зависимости процесса Е и предэкспоненту К0 находят из соотношений:
E = R×h16; (114)
K0 = expg16. (115)
8.7.8.
Рассчитывают показатель ![]() по уравнению (104),
используя полученные параметры
по уравнению (104),
используя полученные параметры ![]() ,
, ![]()
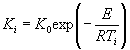 .
.
8.7.9. Среднюю квадратичную ошибку аппроксимации экспериментальных данных уравнением (104) для всех температур вычисляют по формуле:
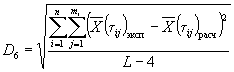 . (116)
. (116)
8.8. Зависимость
изменения показателя ![]() от продолжительности
испытаний при каждой из температур, обрабатывают в соответствии с п. 8.7.
от продолжительности
испытаний при каждой из температур, обрабатывают в соответствии с п. 8.7.
8.8.1.
Значение ![]() определяют в
соответствии с п. 8.7.1.
определяют в
соответствии с п. 8.7.1.
8.8.2.
Зависимость ![]() от tij, полученную в эксперименте,
описывают кинетическим уравнением вида:
от tij, полученную в эксперименте,
описывают кинетическим уравнением вида:
где f = 1, 2, ..., и - количество экспонент.
8.8.3. Для каждой температуры при всех съемах вычисляют вспомогательную функцию вида:
![]() . (118)
. (118)
Зависимость
![]() от продолжительности
испытаний при каждой температуре описывают линейным уравнением вида:
от продолжительности
испытаний при каждой температуре описывают линейным уравнением вида:
и вычисляют коэффициенты уравнения (119) методом наименьших квадратов по формулам:
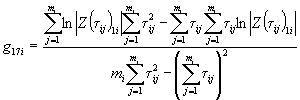 ; (120)
; (120)
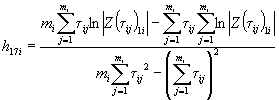 . (121)
. (121)
8.8.4. Вычисляют значения параметров K1i и g1i уравнения (117) с одной экспонентой для каждой температуры по соотношениям:
![]() ; (122)
; (122)
![]() . (123)
. (123)
Значение ![]() вычисляют по формуле
вычисляют по формуле
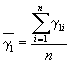 . (124)
. (124)
8.8.5.
Зависимость lnК1i от ![]() описывают линейным
уравнением вида:
описывают линейным
уравнением вида:
и вычисляют коэффициенты g18 и h18 уравнения (125) методом наименьших квадратов:
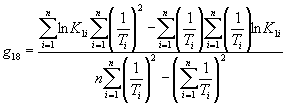 ; (126)
; (126)
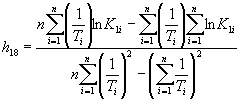 . (127)
. (127)
8.8.6. Коэффициент E1 и предэкспоненту K0i находят из соотношений:
E1 = Rh18; (128)
K01 = expg18. (129)
8.8.7.
Вычисляют значение ![]() по формуле (117),
используя значения
параметров:
по формуле (117),
используя значения
параметров:
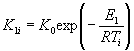 ;
; ![]() ;
; ![]() .
.
8.8.8. Вычисляют среднюю квадратическую ошибку аппроксимации экспериментальных данных для всех температур уравнением (117), содержащим одну экспоненту по формуле
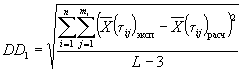 , (130)
, (130)
где ![]() - значения
показателя, вычисленные по уравнению (117) при одной экспоненте с
параметрами
- значения
показателя, вычисленные по уравнению (117) при одной экспоненте с
параметрами ![]() ;
; ![]() ; K1i.
; K1i.
8.8.9.
Вычисляют вспомогательную функцию ![]() для каждой
температуры, когда уравнение (117) содержит 2 экспоненты:
для каждой
температуры, когда уравнение (117) содержит 2 экспоненты:
![]() . (131)
. (131)
8.8.10.
Зависимость ![]() от tij описывают линейным уравнением
вида:
от tij описывают линейным уравнением
вида:
и вычисляют коэффициенты уравнения (132) методом наименьших квадратов:
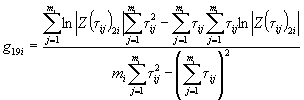 ; (133)
; (133)
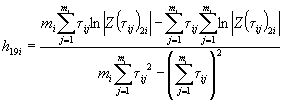 . (134)
. (134)
8.8.11. Вычисляют параметры K2i и g2i второй экспоненты уравнения (117) по соотношениям:
![]() ; (135)
; (135)
![]() . (136)
. (136)
Значение ![]() вычисляют по формуле
вычисляют по формуле
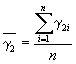 . (137)
. (137)
8.8.12.
Зависимость lnК2i от ![]() описывают линейным
уравнением вида:
описывают линейным
уравнением вида:
и вычисляют коэффициенты уравнения (138) методом наименьших квадратов.
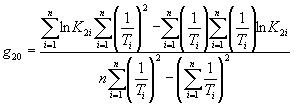 ; (139)
; (139)
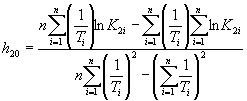 . (140)
. (140)
8.8.13. Коэффициент Е2 и предэкспоненту К02 находят из соотношений:
E2 = R×h20; (141)
K02 = expg20. (142)
Вычисляют
![]() по формуле (117)
используя параметры
по формуле (117)
используя параметры
![]() ;
; ![]() ;
; ![]() ;
; 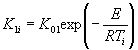 ;
; 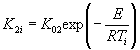 .
.
8.8.14. Среднюю квадратическую ошибку аппроксимации экспериментальных данных при всех температурах уравнением (117), содержащим две экспоненты, вычисляют по формуле
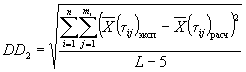 . (143)
. (143)
8.8.15.
Увеличивают количество экспонент в уравнении (117) и вычисляют
вспомогательные функции ![]() при каждой
температуре по формуле
при каждой
температуре по формуле
![]() . (144)
. (144)
Вычисление
![]() с последующим
вычислением
с последующим
вычислением ![]() и
и ![]() продолжают до тех
пор, пока
продолжают до тех
пор, пока
![]() , (145)
, (145)
где DDu и DDu-1 - средние квадратические ошибки аппроксимации экспериментальных данных уравнением (117) при количестве экспонент u и u-1 соответственно.
8.9. Если выбранное кинетическое уравнение удовлетворительно описывает экспериментальные данные, то для вычисленных коэффициентов температурной зависимости (Е) определяют значение эквивалентной температуры (Тэ) в соответствии с приложением 5.
8.10. Вычисляют значения констант скоростей процессов при Тэ, определенных по п. 8.9, по формуле
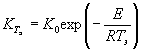 . (146)
. (146)
Если в
выбранном уравнении несколько констант скоростей процессов, ![]() вычисляют для
каждого из выявленных процессов.
вычисляют для
каждого из выявленных процессов.
Если
прогнозирование изменения показателя проводят уравнением (17),
предварительно вычисляют ![]() по формуле
по формуле
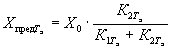 . (147)
. (147)
8.11.
Подставляют значения ![]() и других
параметров в выбранное кинетическое уравнение и вычисляют значения показателя
и других
параметров в выбранное кинетическое уравнение и вычисляют значения показателя ![]() для значений tхр с шагом
365 суток.
для значений tхр с шагом
365 суток.
8.12.
Относительное изменение показателя ![]() для каждого
срока хранения tхр
вычисляют по формуле
для каждого
срока хранения tхр
вычисляют по формуле
![]() . (148)
. (148)
Значение ![]() записывают в таблицу,
по которой прогнозируют изменение показателя за любой срок хранения при
эквивалентной температуре, или по заданному сроку хранения в этих условиях
прогнозируют изменение показателя в пределах изменений, полученных
экспериментально.
записывают в таблицу,
по которой прогнозируют изменение показателя за любой срок хранения при
эквивалентной температуре, или по заданному сроку хранения в этих условиях
прогнозируют изменение показателя в пределах изменений, полученных
экспериментально.
8.13. Держателем программы обработки результатов ускоренных испытаний полимерных материалов по методу 1 на ЭВМ типа ЕС является НПО «ИСАРИ».
Разд. 8. (Введен дополнительно, Изм. № 1).
ПРИЛОЖЕНИЕ 8
Справочное
СПОСОБ ГРАФИЧЕСКОГО ДИФФЕРЕНЦИРОВАНИЯ
Геометрически дифференциал изображается приращением X ординаты точки на касательной к графику функции X = f(t), как показано на черт. 1.
Черт. 1
Графическое дифференцирование проводят на криволинейном участке, полученной при испытаниях кинетической зависимости X от t, где наблюдается заметное изменение скорости процесса.
Пример применения способа графического дифференцирования.
Кривая, приведенная на черт. 2, является графиком зависимости X от t. Необходимо способом графического дифференцирования определить производные этой функции в точках а, b, с, d, e.
Черт. 2
1. Для удобства дифференцирования а, b, с, d, e выбирают на кривой так, чтобы проекции отрезков Х0а, ab, bc, cd, de, были равны.
2. В
точках a, b, с, d, e с абсциссами t1, t2, t3, t4, t5 проводят касательные к кривой. Рассматривают
треугольники: аа¢а², bb¢b", сс¢с", dd¢d", ee¢e". Производные
в точках а, b, с, d, e будут соответственно равны отношениям сторон
треугольников ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Отрезки а¢а", b¢bb", с¢с", e¢e", d¢dd" измеряют в единицах измерения, принятых для оси ординат; отрезки a¢a, b¢b, c¢c, d¢d, e¢e - в единицах измерения, принятых для оси абсцисс.
ПРИЛОЖЕНИЕ 9
Справочное
ПРИМЕР ОБРАБОТКИ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ В СЛУЧАЕ ДВУХ НЕКОНКУРИРУЮЩИХ ПРОЦЕССОВ ПЕРВОГО ПОРЯДКА
1. Необходимо описать кривую прогноза изменения показателя от продолжительности хранения под навесом в условиях очень жаркого сухого климата по результатам испытаний, полученных по методу 1 настоящего стандарта.
Условия и результаты испытаний указаны в табл. 1.
Таблица 1
|
Температура испытаний t, °С |
Продолжительность испытаний t, сут |
Значение показателя X (остаточная деформация eост, %) |
Температура испытании t, °С |
Продолжительность испытаний t, сут |
Значение показателя X (остаточная деформация eост, %) |
|
50 |
0 |
0 |
70 |
0 |
0 |
|
15 |
20 |
10 |
38 |
||
|
30 |
35 |
20 |
50 |
||
|
60 |
41 |
45 |
67 |
||
|
90 |
46 |
90 |
81 |
||
|
120 |
56 |
120 |
90 |
||
|
150 |
57 |
- |
- |
||
|
180 |
61 |
- |
- |
||
|
60 |
0 |
0 |
90 |
0 |
0 |
|
30 |
31 |
5 |
50 |
||
|
60 |
53 |
10 |
66 |
||
|
100 |
64 |
20 |
78 |
||
|
140 |
73 |
30 |
86 |
||
|
- |
- |
40 |
90 |
2. Для каждой из температур строят графики зависимости изменения показателя Х от продолжительности испытаний t, как показано на черт. 1. Поскольку кривые на черт. 1 указывают на возрастание показателя от продолжительности испытаний, то проверяют правомерность описания этих кинетических кривых уравнением первого порядка для двух неконкурирующих процессов вида
![]() . (1)
. (1)
Черт. 1.
3.
Способом графического дифференцирования, приведенным в справочном приложении 8,
определяют ![]() для каждой из
приведенных на черт. 1 кривых.
для каждой из
приведенных на черт. 1 кривых.
Черт. 2
Данные графического дифференцирования приведены в табл. 2.
Таблица 2
|
Х |
|
Х |
|
X |
|
X |
|
|
при температурах испытаний, °С |
|||||||
|
50 |
60 |
70 |
90 |
||||
|
0,75 |
23 |
0,75 |
35 |
5,50 |
5 |
8,00 |
32 |
|
0,60 |
29 |
0,60 |
41 |
4,50 |
15 |
8,00 |
40 |
|
0,50 |
34 |
0,50 |
47 |
3,50 |
24 |
4,00 |
46 |
|
0,33 |
38 |
0,33 |
52 |
2,40 |
30 |
2,70 |
56 |
|
0,25 |
42 |
0,30 |
57 |
2,00 |
36 |
2,00 |
62 |
|
0,20 |
46 |
0,25 |
63 |
1,50 |
40 |
1,40 |
66 |
|
0,20 |
50 |
0,20 |
68 |
1,50 |
43 |
1,40 |
70 |
|
0,13 |
54 |
0,12 |
72 |
1,00 |
46 |
1,00 |
75 |
|
0,09 |
57 |
- |
- |
1,00 |
51 |
1,00 |
79 |
|
0,09 |
59 |
- |
- |
0,80 |
54 |
1,70 |
82 |
|
- |
- |
- |
- |
0,60 |
61 |
0,50 |
85 |
|
- |
- |
- |
- |
0,30 |
87 |
0,50 |
87 |
4. Строят график зависимости ![]() от X для каждой температуры, как
показано на черт. 2. Экстраполируют линейные участки графика на
значение
от X для каждой температуры, как
показано на черт. 2. Экстраполируют линейные участки графика на
значение ![]() = 0 и
определяют Хпред. Для всех температур Хпред
= 97,5 %.
= 0 и
определяют Хпред. Для всех температур Хпред
= 97,5 %.
5. Строят
графики зависимости ![]() от t для
каждой температуры, как показано на черт. 3.
от t для
каждой температуры, как показано на черт. 3.
Черт. 3
Данные для построения графиков приведены в табл. 3.
По графикам, представленным на черт. 3, определяют lng1, по отрезку, отсекаемому на оси ординат, и константу К1 по тангенсу угла наклона прямой. Для всех температур g1 = 67,5. Значения К1, lnK1 приведены в табл. 4.
Таблица 3
|
t, °с |
t, сут |
Xпред - Х |
ln(Xпред - Х) |
|
50 |
180 |
97,50 - 60 = 37,50 |
3,62 |
|
150 |
97,50 - 57 = 40,50 |
3,70 |
|
|
120 |
97,50 - 56 = 41,50 |
3,72 |
|
|
100 |
97,50 - 50 = 47,50 |
3,86 |
|
|
80 |
97,50 - 46 = 51,50 |
3,94 |
|
|
60 |
97,50 - 41 = 56,50 |
4,03 |
|
|
60 |
140 |
97,50 - 73 = 24,50 |
3,26 |
|
100 |
97,50 - 64 = 33,50 |
3,50 |
|
|
80 |
97,50 - 60 = 37,50 |
3,60 |
|
|
60 |
97,50 - 52 = 45,50 |
3,80 |
|
|
40 |
97,50 - 45 = 52,50 |
3,96 |
|
|
70 |
120 |
97,50 - 90 = 7,50 |
2,01 |
|
110 |
97,50 - 85 = 12,50 |
2,51 |
|
|
100 |
97,50 - 84 = 13,50 |
2,60 |
|
|
90 |
97,50 - 81 = 16,50 |
2,80 |
|
|
80 |
97,50 - 78 = 19,50 |
2,97 |
|
|
70 |
97,50 - 75 = 22,50 |
3,11 |
|
|
60 |
97,50 - 72 = 25,50 |
3,24 |
|
|
50 |
97,50 - 67 = 30,50 |
3,42 |
|
|
40 |
97,50 - 62 = 35,50 |
3,56 |
|
|
90 |
40 |
97,50 - 93 = 4,50 |
1,50 |
|
30 |
97,50 - 87 = 10,50 |
2,35 |
|
|
20 |
97,50 - 77 = 20,50 |
3,00 |
|
|
10 |
97,50 - 65 = 32,50 |
3,48 |
Таблица 4
|
t, °С |
к1 |
lnк1 |
|
50 |
0,004 |
-5,500 |
|
60 |
0,007 |
-4,950 |
|
70 |
0,015 |
-4,200 |
|
90 |
0,059 |
-2,830 |
6. Определяют g2 по уравнению 1; при t = 0 уравнение принимает вид Х0 = Xпред - g1 - g2. Поскольку Х0 = 0, g2 = Xпред - g1 = 97,5 - 67,5 = 30,0.
7. Для определения константы К2 вычисляют функцию
![]()
и строят график зависимости lnZ от t для каждой температуры, как показано на черт. 4.
Черт. 4
Данные для построения графиков зависимости lnZ от t приведены в табл. 5.
Таблица 5
|
t, °с |
t, сут |
Z(t) |
lnZ(t) |
|
50 |
2 |
27,20 |
3,30 |
|
6 |
20,00 |
3,00 |
|
|
10 |
17,40 |
2,85 |
|
|
15 |
12,90 |
2,55 |
|
|
20 |
9,60 |
2,25 |
|
|
60 |
2 |
25,70 |
3,25 |
|
6 |
20,00 |
3,00 |
|
|
10 |
15,90 |
2,75 |
|
|
14 |
12,30 |
2,50 |
|
|
18 |
9,50 |
2,25 |
|
|
70 |
5,00 |
15,85 |
2,75 |
|
10,00 |
7,40 |
2,00 |
|
|
15,00 |
3,50 |
1,25 |
|
|
20,00 |
1,82 |
0,60 |
|
|
90 |
0,50 |
19,10 |
2,95 |
|
1,00 |
11,60 |
2,45 |
|
|
2,00 |
4,50 |
1,50 |
|
|
3,00 |
1,82 |
0,60 |
По тангенсу угла наклона графиков, приведенных на черт. 4, определяют константы К2. Значения констант К2 приведены в табл. 6.
Таблица 6
|
t, °с |
К2 |
lnК2 |
|
50 |
0,046 |
-3,080 |
|
60 |
0,063 |
-2,760 |
|
70 |
0,140 |
-1,960 |
|
90 |
0,920 |
-0,080 |
8. Используя значения констант К1
и К2 для всех температур, строят графики зависимости
lnК2 от ![]() , как показано на черт. 5 и 6.
, как показано на черт. 5 и 6.
9. По тангенсу угла наклона графиков, приведенных на черт. 5 и 6, вычисляют значения коэффициентов Е1 и E2.
Черт. 5
Черт. 6
Е1 = R tga1,
Е2 = R tga2.
Е1 = 68,2 кДж/моль (16,3 ккал/моль),
Е2 = 73,7 кДж/моль (17,6 ккал/моль).
10. Определяют значения эквивалентной температуры Тэ по вычисленным значениям Е1 и E2 и обязательному приложению 5. Коэффициенты Е1 и E2 близки по значениям, поэтому Тэ определяют при Е = 71,2 кДж/моль (17 ккал/моль). Тэ = 295,5 °С.
11. Экстраполируя графики, приведенные на черт. 5 и 6 на Тэ = 295,5 °С, определяют К1 и К2.
lnK1 = -8,1000;
lnK2 = -5,8500;
K1 = 0,0030;
К2 = 0,0029.
12. Используя (1), вычисляют значения показателя Xi при найденных Хпред, g1, g2, K1, K2 и продолжительности хранения 1 - 9 лет (табл. 7).
По данным табл. 7 строят кривую прогноза, как показано на черт. 7.
Таблица 7
|
Значение показателя Xi (eост, %) |
Продолжительность хранения ti, год |
Продолжительность хранения с учетом коэффициента
запаса |
|
0 |
0 |
0,0 |
|
20 |
1 |
0,7 |
|
45 |
2 |
1,3 |
|
50 |
3 |
2,0 |
|
52 |
4 |
2,7 |
|
65 |
5 |
3,3 |
|
68 |
8 |
5,4 |
|
70 |
9 |
6,0 |
Черт. 7
ПРИЛОЖЕНИЕ 10
Рекомендуемое
МЕТОД СОЗДАНИЯ ПОСТОЯННОГО ЗНАЧЕНИЯ ВЛАЖНОСТИ ВОЗДУХА НАД РАСТВОРАМИ СОЛЕЙ
1. Метод создания постоянного значения влажности воздуха в испытательной камере основан на выдержке образцов над растворами солей. Растворы солей приведены в таблице.
|
Наименование общества |
Концентрация водного раствора |
Абсолютная влажность воздуха, г/м3 |
Относительная влажность воздуха, % |
|
Кальций хлористый 6-водный СаСl2×6H2O квалификации х. ч. |
Насыщенный раствор |
5,3 ± 1,0 |
30 ± 2 |
|
Натрий двухромовокислый Na2Cr2O7×2Н2О квалификации ч. д. а. по ГОСТ 4237-76 и натрий сернокислый NaHS04×H2O квалификации ч. д. а. по ГОСТ 6053-77 |
Насыщенный раствор, соотношение солей в растворе 1:1 |
8,6 ± 1,6 |
50 ± 2 |
|
Натрий азотистокислый NаNO2 квалификации ч. по ГОСТ 4197-74 |
Насыщенный раствор |
11,3 ± 1,7 |
65 ± 2 |
|
Медь (II) сернокислая 5-водная CuSO4×5H20 квалификации ч. д. а. по ГОСТ 4165-78 |
Насыщенный раствор |
16,8 ± 2,4 |
98 ± 1 |
2. Раствор для создания заданной влажности, приготовленный при температуре (293±2) К (20±2) °С в соответствии с таблицей, наливают на дно камеры.
Для равномерного распределения влажности воздуха в камере высота ее не должна превышать длины меньшей стороны прямоугольной поверхности зеркала испарения.
Общая площадь поверхности кондиционируемых образцов не должна превышать общей площади поверхности раствора; для пленочных материалов общая площадь поверхности образцов не должна превышать площади зеркала раствора более чем в 3 раза.
ПРИЛОЖЕНИЕ 11
Обязательное
МЕТОД ОПРЕДЕЛЕНИЯ ЗАДАННОГО ЗНАЧЕНИЯ ВЛАЖНОСТИ ВОЗДУХА, ПРИ КОТОРОМ МАССОВАЯ ДОЛЯ ВЛАГИ В ОБРАЗЦАХ СОХРАНЯЕТСЯ ПОСТОЯННОЙ
Сущность метода состоит в определении значения влажности воздуха в рабочем объеме испытательной камеры при заданной температуре испытаний, обеспечивающего постоянное значение массовой доли влаги в образце.
1. Отбор образцов
Образцы должны соответствовать требованиям п. 1.2.2 настоящего стандарта.
Количество образцов для испытаний не должно быть менее 25.
2. Аппаратура
Испытательная камера и весы в соответствии с требованиями п. 1.2.2 настоящего стандарта.
3. Проведение испытаний
Кондиционирование проводят до достижения в образцах постоянной массовой доли влаги путем периодического взвешивания с предельной допускаемой погрешностью ±0,01 %. Периодичность кондиционирования 72 ч. Кондиционирование прекращают, если за последние 72 ч изменение массы образцов не превышает 5 % от полного изменения их массы за всю продолжительность кондиционирования.
Определяют массу каждого образца, достигшего постоянного значения массовой доли влаги.
3.2. В пяти испытательных камерах устанавливают одно и то же значение температуры испытаний, выбранное по п. 2.5.1.2 настоящего стандарта, и разные значения относительной влажности воздуха, которые выбирают из ряда: 20, 30, 40, 50, 60 %.
3.3. В каждую из испытательных камер, подготовленных по п. 3.2, помещают по 5 образцов после их кондиционирования по п. 3.1. Периодически, через каждые 72 ч выдержки, образцы извлекают из испытательных камер, охлаждают до температуры (293±2) К (20±2) °С в течение 30 мин и взвешивают с предельной допускаемой погрешностью ±0,01 %. Выдержку прекращают, если за последние 72 ч изменение массы образцов не превышает 5 % от полного изменения массы за всю продолжительность выдержки.
4. Обработка результатов
4.1. Вычисляют исходное суммарное значение массы образцов, помещенных в каждую испытательную камеру, после кондиционирования по п. 3.1.
4.2. Вычисляют суммарное значение массы образцов после выдержки в каждой камере по п. 3.3 при каждом значении влажности воздуха, установленном по п. 3.2.
4.3. За значение относительной влажности воздуха при заданной температуре испытаний, при котором массовая доля влаги в образце сохраняется постоянной, принимают влажность воздуха в той камере, значение массы образцов в которой, определенное по п. 4.2, отличается от исходного значения, определенного по п. 4.1, не более чем на 0,02 %.
ПРИЛОЖЕНИЕ 12
Справочное
КОЛИЧЕСТВО ПЕРЕХОДОВ ТЕМПЕРАТУРЫ ЧЕРЕЗ 273 К (0 °С) ДЛЯ НЕОТАПЛИВАЕМЫХ ХРАНИЛИЩ В ТЕЧЕНИЕ ОДНОГО ГОДА ХРАНЕНИЯ
|
Климатический район |
Тип хранилища |
Количество переходов через 273 К (0 °С) |
|
|
Среднее значение |
Стандартное отклонение |
||
|
Холодный |
А |
9 |
2 |
|
Б |
8 |
2 |
|
|
Умеренный |
А |
8 |
3 |
|
Б |
6 |
2 |
|
|
Жаркий, сухой |
A |
5 |
2 |
Примечание. А - неотапливаемое хранилище кирпичного или блочного типа без потолочного перекрытия; Б - неотапливаемое хранилище кирпичного или блочного типа с потолочным перекрытием.
ПРИЛОЖЕНИЕ 13
Справочное
ПРОТОКОЛ ИСПЫТАНИЙ
|
Номер образца |
Значение показателя исследуемого материала |
Значение показателя материала - аналога |
||||||
|
Исходное |
После испытаний в режиме |
Исходное |
После испытаний в режиме |
|||||
|
1 |
2 |
3 |
1 |
1 |
3 |
|||
|
Х0 |
|
|
Х3 |
Y0 |
|
|
Y3 |
|
|
|
|
|
|
|
|
|
|
|
ПРИЛОЖЕНИЕ 14
Рекомендуемое
АЛГОРИТМ ОПРЕДЕЛЕНИЯ НА ЭВМ ПРОДОЛЖИТЕЛЬНОСТИ ВОЗДЕЙСТВИЯ ПОЛОЖИТЕЛЬНОЙ ТЕМПЕРАТУРЫ tу ПРИ УСКОРЕННЫХ ИСПЫТАНИЯХ ПО МЕТОДУ 2
Алгоритм предназначен для вычисления продолжительности ускоренных испытаний tу (при воздействии положительной температуры испытаний Ту), эквивалентной продолжительности хранения и (или) эксплуатации tхр при эквивалентной температуре Тэ.
1. Алгоритм предназначен для вычисления tу по п. 2.5.1.5 настоящего стандарта, если кинетические уравнения (46, 70) или разд. 8 приложения 7 удовлетворительно описывают экспериментальные данные.
2. Если экспериментальные данные описывают уравнением (70) разд. 8 приложения 7, то tу определяют в соответствии с требованиями, изложенными ниже.
2.1.
Вычисляют значение ![]() по формуле (70)
разд. 8
приложения 7 при эквивалентной температуре
хранения Tэ и
заданной продолжительности хранения tхр.
по формуле (70)
разд. 8
приложения 7 при эквивалентной температуре
хранения Tэ и
заданной продолжительности хранения tхр.
2.2.
Вычисляют ![]() по формуле
по формуле
где параметры ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответствуют параметрам
уравнения 70
при эквивалентной температуре.
соответствуют параметрам
уравнения 70
при эквивалентной температуре.
2.3. Определяют знак функции F(ty) при tу = 0 по формуле
Параметры ![]() , K1y,
, K1y, ![]() , K2y,
, K2y, ![]() и
и ![]() соответствуют
параметрам уравнения (70) разд. 8 приложения 7,
вычисленными при Тэ и Ту.
соответствуют
параметрам уравнения (70) разд. 8 приложения 7,
вычисленными при Тэ и Ту.
2.4. Значение tу, при котором значение F(ty) равно нулю, определяют в соответствии с требованиями, изложенными ниже.
2.4.1. Вычисляют значение функции F(ty) по формуле (2), увеличивая значение tу на 15 сут.
2.4.2. Если знак функции F(ty) остается тем же, что и знак этой функции, вычисленной по п. 2.3, то продолжают вычисление функции F(ty), увеличивая продолжительность tу на шаг 15 сут до тех пор, пока знак функции F(ty) изменится на противоположный.
2.4.3. Вычисляют значение функции F(ty) при уменьшении tу на половину предыдущего шага. Если знак функции F(ty) остается тем же, вычисляют значение функции F(ty) при уменьшении tу на половину предыдущего шага. Вычисления продолжают до тех пор, пока либо изменится знак функции, либо значение шага уменьшения tу будет меньше 0,5 сут.
2.4.4. Если знак функции F(ty), вычисленный по п. 2.4.3, изменится на противоположный, вычисляют функцию F(ty) при увеличении tу на половину предыдущего шага. Вычисления функции продолжают до тех пор, пока либо изменится знак функции, либо значение шага увеличения tу будет меньше 0,5 сут.
2.4.5. Если знак функции F(ty), вычисленный по п. 2.4.4, изменится на противоположный, то вычисления функции F(ty) продолжают по пп. 2.4.3 и 2.4.4 до тех пор, пака значение изменения tу между последующим и предыдущим вычислением будет меньше 0,5 сут.
Полученное значение tу принимают за продолжительность ускоренных испытаний при Ту, эквивалентную tхр при Тэ при этом tу должна быть не более tу(max) = 1200 сут.
3. Если экспериментальные данные описывают уравнением (46) разд. 8 приложения 7, tу вычисляют по пп. 2.3 - 2.4.5, заменяя F(ty) нa
![]() , (3)
, (3)
где параметры K1y, K2y, ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответствуют
параметрам уравнения (46) приложения 7, вычисленным для Ту
и Тэ.
соответствуют
параметрам уравнения (46) приложения 7, вычисленным для Ту
и Тэ.
4. Если экспериментальные данные описывают уравнением (117) разд. 8 приложения 7, tу вычисляют по пп. 2.3 - 2.4.5, заменяя F2(ty) на
![]() , (4)
, (4)
где параметры ![]() ,
, ![]() ,
, ![]() соответствуют
параметрам уравнения (117) разд. 8 приложения 7, вычисленным при Тэ
и Ту.
соответствуют
параметрам уравнения (117) разд. 8 приложения 7, вычисленным при Тэ
и Ту.
5. Держателем Программы определения продолжительности ускоренных испытаний по методу 2 на ЭВМ типа ЕС является НПО «ИСАРИ».
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАН И ВНЕСЕН Государственным комитетом СССР по стандартам
РАЗРАБОТЧИКИ
X.Н. Фидлер, канд. техн. наук; В.Д. Гойхман д-р техн. наук; Д.В. Замбахидзе, канд. техн. наук; О.А. Хачатурова; А.Г. Попов, канд. техн. наук; Т.П. Смехунова, канд. техн. наук; А.М. Грищенко, канд. техн. наук; И.Я. Гунин; Л.П. Котова; О.Н. Якунина
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 25.12.81 № 5664
3. ВВЕДЕН ВПЕРВЫЕ
4. ПРОВЕРЕН В 1989 г.
5. Требования стандарта в части определения количества образцов и статической обработки результатов испытаний соответствуют СТ СЭВ 983-73
6. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
|
Обозначение НТД, на который дана ссылка |
Номер пункта, приложения |
|
Приложение 1 |
|
|
ГОСТ 8.221-76 |
Приложение 1 |
|
Приложение 1 |
|
|
ГОСТ 4237-76 |
Приложение 4 |
|
ГОСТ 6053-77 |
Приложение 10 |
|
Вводная часть; Приложение 5 |
|
|
ГОСТ 24482-80 |
7. ПЕРЕИЗДАНИЕ (март 1990 г.) с Изменением № 1, утвержденным в июле 1989 г. (ИУС 12-89)
8. Срок действия продлен до 01.07.95 Постановлением Госстандарта СССР от 22.08.89 № 2609
СОДЕРЖАНИЕ