
Приказ
Федеральной службы по экологическому, технологическому и атомному надзору
от 8 июня 2010 г. № 465
"Об утверждении Положения о повышении точности прогностических оценок
радиационных характеристик радиоактивного загрязнения окружающей среды и
дозовых нагрузок на персонал и население"
В целях реализации полномочий, установленных в пунктах 5.3.1.1 - 5.3.1.4, 5.3.1.13, 5.3.2, 6.2 Положения о Федеральной службе по экологическому, технологическому и атомному надзору, утвержденного постановлением Правительства Российской Федерации от 30 июля 2004 г. № 401, приказываю:
1. Утвердить прилагаемое Положение о повышении точности прогностических оценок радиационных характеристик радиоактивного загрязнения окружающей среды и дозовых нагрузок на персонал и население.
2. Признать утратившим силу приказ Федеральной службы по экологическому, технологическому и атомному надзору от 15 января 2010 г. № 11 "Об утверждении Положения о повышении точности прогностических оценок радиационных характеристик радиоактивного загрязнения окружающей среды и дозовых нагрузок на персонал и население".
|
Врио руководителя |
Б.А. Красных |
Содержание
Положение
о повышении точности прогностических оценок радиационных характеристик
радиоактивного загрязнения окружающей среды и дозовых нагрузок на персонал и
население
(утв. приказом Федеральной службы по экологическому, технологическому и
атомному надзору от 8 июня 2010 г. № 465)
I. Общие положения
1. Настоящее Положение о повышении точности прогностических оценок радиационных характеристик радиоактивного загрязнения окружающей среды и дозовых нагрузок на персонал и население (далее - Положение) входит в число руководств по безопасности, носит рекомендательный характер и не является нормативным правовым актом.
2. Настоящее Положение содержит рекомендации Федеральной службы по экологическому, технологическому и атомному надзору по использованию расчетных методов прогнозирования радиационных характеристик радиоактивного загрязнения окружающей среды и дозовых нагрузок на персонал и население, включая рекомендации:
по обоснованию того, что использование показаний детекторов фотонного излучения, наряду с расчетными данными, позволяет значительно повысить точность прогнозирования расчетных оценок радиоактивного загрязнения окружающей среды, а погрешность расчетов свести к погрешности детектора;
по формулировке основных принципов и выбору критериев для оптимального размещения постов радиационного контроля на промплощадке и в санитарно-защитной зоне (далее - СЗЗ) атомной электростанции (далее - АС), позволяющих минимизировать последствия радиационных аварий;
по выбору алгоритма, способствующего повышению точности прогностических оценок радиационных характеристик радиоактивного загрязнения окружающей среды, для определения координат детектора фотонного излучения, расположенного на промплощадке и в СЗЗ АС.
3. Использование рекомендаций настоящего Положения направлено на решение следующих основных задач:
оптимизацию финансовых затрат на разработку автоматизированных систем контроля радиационной обстановки (далее - АСКРО) АС и объектов использования атомной энергии (далее - ОИАЭ);
осуществление прогнозирования результатов радиоактивного загрязнения окружающей среды при отсутствии информации о радионуклидном составе радиоактивной примеси, выброшенной в атмосферу, в условиях радиационных аварий на АС или любом другом ОИАЭ, на котором внедрена АСКРО с учетом рекомендаций настоящего Положения;
повышение точности прогнозирования результатов радиоактивного загрязнения окружающей среды и дозовых нагрузок на персонал и население при радиационных авариях на АС или других ОИАЭ.
II. Рекомендации к составу и условиям работы АСКРО
4. Основу АСКРО составляют: система постов контроля мощности дозы фотонного излучения, размещаемых на местности; совокупность датчиков, измеряющих метеопараметры, по показаниям которых определяется состояние устойчивости атмосферы; технологические датчики АС, предназначенные для определения параметров выброса радиоактивной примеси в атмосферу; программное обеспечение нижнего и верхнего уровней, из которых первое обеспечивает обработку данных (показаний датчиков) с целью преобразования их в специальный формат - для использования в качестве исходных данных при проведении прогностических расчетов. Основу программного обеспечения верхнего уровня составляют расчетные модели переноса радиоактивной примеси в атмосфере и водной среде, а также математические методы оценки дозовых нагрузок на персонал и население. С его помощью непосредственно осуществляются прогностические расчеты радиоактивного загрязнения окружающей среды. Структурная схема состава АСКРО приведена на рис. 1 Приложения № 1.
5. Функционирование АСКРО рекомендуется осуществлять в режиме реального времени, что достигается путем автоматизации сбора данных по радиационным и метеорологическим параметрам, на основе которых осуществляются прогностические расчеты с использованием математических моделей распространения радиоактивной примеси в воздушной и водной средах при выбросах АС.
6. При проектировании АСКРО необходимо принимать во внимание экономические, экологические, физико-технические критерии, а также демографические особенности региона, где размещена АС. Указанные критерии, отвечающие условиям размещения постов радиационного контроля на промплощадке и в СЗЗ ОИАЭ, приведены в Приложении № 2.
7. Погрешность прогностических оценок радиоактивного загрязнения окружающей среды и дозовых нагрузок на персонал и население, получаемых с помощью расчетных моделей, может быть минимизирована за счет уточнения метеопараметров атмосферы, использования показаний детекторов фотонного излучения АСКРО и уточнения величины мощности выброса газоаэрозольной радиоактивной примеси (PВ), поступающей в атмосферу, в условиях радиационных аварий и при штатной работе.
III. Определение метеорологических параметров для оценки условий формирования радиационной обстановки на местности
8. Особую роль в оценке состояния устойчивости пограничного слоя атмосферы играют определяющие его метеорологические параметры: скорость ветра, температура, влажность и т.д. Изменение одного из этих параметров непременно ведет и к изменению состояния устойчивости пограничного слоя в целом, а это, в свою очередь, - к изменению концентрации радиоактивной примеси и изменению радиационной обстановки на местности.
9. Определение метеорологических параметров, применительно к региону, в котором расположена АС, целесообразно осуществлять на специальных метеоплощадках лабораторий внешней дозиметрии.
10. Измерение направления, скорости ветра, температуры и влажности рекомендуется проводить на нескольких уровнях на метеомачте, расположенной на метеоплощадке лаборатории внешней дозиметрии, применяя методику градиентных наблюдений. измеренные параметры в дальнейшем могут быть использованы как реперные точки для расчета полных профилей этих величин в пограничном слое атмосферы в более совершенных метеорологических моделях или как постоянные - непосредственно в уравнениях, на основании которых рассчитывают распределение радиоактивной примеси в атмосфере при ее переносе. Методика обработки градиентных наблюдений приведена в Приложении № 3, а в приложении № 4 приведены методы вычислений метеопараметров.
IV. Рекомендации по использованию моделей переноса радиоактивной примеси в атмосфере
11. Выбор модели переноса радиоактивной примеси в атмосфере рекомендуется осуществлять на основании:
1) результатов прогностического расчета радиоактивного загрязнения окружающей среды и дозовых нагрузок на персонал и население с "удовлетворительной (наименьшей) погрешностью" на расстояниях не менее 30 км от источника выбросов при любой эффективной высоте источника радиоактивного загрязнения, не превышающей высоту пограничного слоя атмосферы с учетом:
особенности подстилающей поверхности, определяющей величину скорости сухого осаждения (значения скорости сухого осаждения для различных нуклидов и типов поверхности приведены в Приложении № 5);
параметра шероховатости (значения параметра шероховатости для различных типов подстилающих поверхностей приведены в Приложении № 6);
вымывания радиоактивной примеси естественными осадками (дождем, снегом) и туманом (значения постоянной вымывания радиоактивной примеси естественными осадками и туманом приведены в Приложении № 7);
радиоактивного распада примеси во время переноса (значения постоянной распада радиоактивной примеси для основных радионуклидов, выбрасываемых в атмосферу АС и другими ОИАЭ приведены в Приложении № 8);
влажности атмосферы;
дисперсного состава примеси или скорости гравитационного осаждения (формулы для расчета скорости гравитационного осаждения частицы приведены в Приложении № 9);
значений метеопараметров (продольной и поперечной скорости ветра, коэффициента турбулентной диффузии, энергии турбулентных пульсаций) по всему пограничному слою атмосферы;
мощности выброса радиоактивной примеси в атмосферу.
2) использования аттестованных методик для определения метеорологических параметров модели (основные рекомендации к датчикам метеопараметров приведены в Приложении № 10).
3) проведения в режиме реального времени прогностических оценок радиоактивного загрязнения окружающей среды и дозовых нагрузок на персонал и население (расчет по модели со всеми функционалами, определяющими дозовые нагрузки на персонал и население и масштабы загрязнения окружающей среды в стационарных условиях, не может превышать время, необходимое на получение осредненных значений измеренных величин метеопараметров ~ 10 мин).
4) экономического фактора, суть которого применительно к данному случаю состоит в том, что предпочтение рекомендуется отдавать такой модели, которая, не ухудшая параметры системы и точность прогнозирования, позволяет уменьшить затраты на оборудование.
V. Параметры модели
12. Одним из основных параметров модели является величина мощности выброса радиоактивной примеси (PВ), поступающей в атмосферу из отверстий (щелей, трещин, клапанов, разрывов) при авариях на АС.
13. Для определения указанного параметра в режиме реального времени проектирующим организациям рекомендуется использовать новые разработки приборов, обеспечивающих измерение PВ не только общей активности газоаэрозольной примеси, но и парциальных величин при выбросе примеси, состоящей из нескольких радионуклидов, а при отсутствии подобных приборов, проводить НИОКР с целью их разработки.
14. При отсутствии соответствующей аппаратуры для определения PВ последнюю рекомендуется оценивать путем сравнения расчетного и измеренного значений мощности дозы внешнего облучения, создаваемого потоком фотонного излучения радионуклидов радиоактивной примеси в точке, ближайшей к оси выброса, если априори известен ее состав и радиационные характеристики радионуклидов. Однако точность подобных оценок величины PВ будет существенно ниже, чем при ее приборном измерении.
VI. Методы прогнозирования
15. Радиационные характеристики радиоактивного загрязнения окружающей среды: мощность дозы от объемного источника (факела или облака выбросов), поверхностная активность подстилающей поверхности, мощность дозы от подстилающей поверхности, доза при ингаляции и т.д. - определяются как функционалы полученного решения для концентрации радиоактивной примеси, радионуклидный состав которой определен.
16. При оценке таких радиационных характеристик, как мощности дозы внешнего облучения от объемного источника (радиоактивного облака) и подстилающей поверхности, загрязненной в результате осаждения радиоактивной примеси, рекомендуется использовать интегральные методы. Это позволит не только избежать погрешности при оценке указанных величин, связанной с нарушением закона лучевого равновесия на границе раздела сред воздух-земля, но и найти ряд особенностей в пространственном распределении этих величин, обусловленных переносом примеси в атмосфере при различных ее метеорологических состояниях. При этом знание величины PВ позволяет существенно скорректировать расчетные оценки пространственных распределений мощности дозы, активности подстилающей поверхности и других радиационных характеристик.
17. Для оценок радиационной обстановки в районе действующей АС, рекомендуется использовать математические методы, изложенные в Приложениях № 11-15, физические основы которых представлены в приложениях № 16-18, а также технические средства, рассматриваемые в Приложении № 19.
18. Мониторинг, основанный на использовании автоматизированных технических средств, является альтернативой математическим методам прогнозирования радиационной обстановки информативность подобной автоматизированной системы напрямую зависит от числа постов контроля, оборудованных датчиками, регистрирующими ионизирующее излучение.
VII. Условия необходимого и достаточного количества датчиков АСКРО, размещаемых на промплощадке и в СЗЗ ОИАЭ
19. Для определения необходимого и достаточного числа датчиков, способных зарегистрировать факел или облако радиоактивных выбросов, распространяющихся от источника при любых направлении ветра и состоянии устойчивости атмосферы, рекомендуется воспользоваться алгоритмом, изложенным в приложении № 20.
VIII. Принцип размещения детекторов фотонного излучения АСКРО на промплощадке и в СЗЗ ОИАЭ
20. Радиоактивное загрязнение окружающей среды при несанкционированном выбросе радиоактивной примеси в виде перегретой газовой струи из отверстий, клапанов, неплотностей сосудов, рваных отверстий или щелей, возникающих в случае взрыва или разрыва резервуаров, находящихся под высоким давлением и высокой температурой, или в случае мощного импульсного выброса радиоактивной примеси через отверстия (например, при проведении учений на АС рассматривается отверстие в потолочном перекрытии реактора (РБМК), возникающее при падении инородного предмета с воздуха), когда полностью отсутствует информация о радионуклидном составе примеси или спектральном составе ее фотонного излучения, рекомендуется оценивать по показаниям технологических датчиков, устанавливаемых в резервуарах и определяющих температуру и давление среды, и датчиков АСКРО, определяющих мощность дозы внешнего облучения от радиоактивного облака, образовавшегося в результате выброса. При этом датчики на промплощадке и в СЗЗ рекомендуется располагать таким образом, чтобы расстояние от возможного источника радиационной опасности (АС) до любого из датчиков было строго различно. Например, последовательность значений указанных расстояний (от минимального до максимального) могла бы подчиняться формуле спирали Архимеда. Принцип размещения детекторов фотонного излучения АСКРО на промплощадке и в СЗЗ ОИАЭ более подробно рассмотрен в Приложении № 21.
21. Для оперативной оценки радиоактивного загрязнения окружающей среды при отсутствии информации о радионуклидном составе радиоактивной примеси, формирующей радиоактивное облако с учетом расстановки детекторов фотонного излучения системы АСКРО равномерно по азимуту и на различных расстояниях от источника, рекомендуется определить спектральный состав фотонного излучения радиоактивной примеси и его среднюю энергию, для чего рекомендуется воспользоваться алгоритмом, приведенным в Приложении № 21.
IX. Уточнение величины PВ
22. Одним из основных параметров модели переноса газоаэрозольной радиоактивной примеси в атмосфере, как отмечалось в пункте 12 настоящего Положения, является величина PВ радиоактивной примеси, поступающей в атмосферу при радиационных авариях на АС или любом другом ОИАЭ. Уточнение этого параметра позволяет скорректировать все остальные характеристики радиоактивного загрязнения окружающей среды (величину объемной активности радиоактивной примеси, распространяющейся в воздушном бассейне, и масштаб радиоактивного загрязнения окружающей среды в целом). Метод уточнения величины PВ, а также более точная оценка величины PВ с учетом фоновых значений мощности дозы естественного или техногенного происхождения приведены в Приложении № 22.
X. Выбор датчика для уточнения величины PВ
23. Для получения более точного значения PВ ее рекомендуется определять по показанию детектора АСКРО при условии их достаточного числа в СЗЗ, ближайшего к оси выброса в соответствии с рис. 1 Приложения № 23.
24. Определение датчика, ближайшего к оси выброса, рекомендуется проводить по алгоритму, изложенному в Приложении № 23.
25. Пример алгоритма прогностических расчетов загрязнения окружающей среды с оценкой дозовых нагрузок на персонал и население приведен на рис. 2 Приложения № 23.
26. Термины и определения, используемые в настоящем документе, приведены в Приложении № 24.
Приложение № 1
Структурная схема состава АСКРО
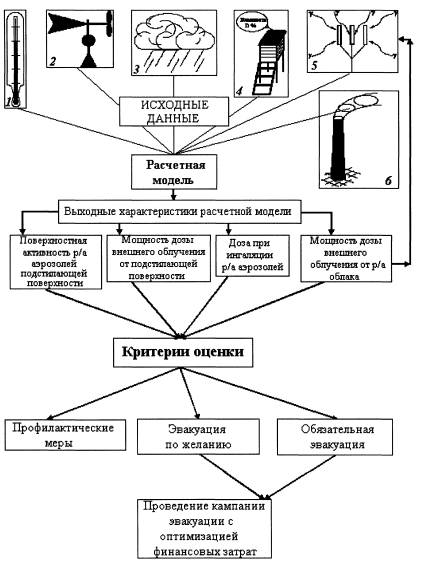
Рис. 1 Структурная схема АСКРО: 1 -датчики температуры окружающей среды; 2 - датчики направления и скорости ветра; 3 - датчики осадков; 4 - датчики влажности окружающей среды; 5 –датчики фотонного излучения постов контроля; 6 - технологические датчики параметров выброса радиоактивной примеси в атмосферу.
Приложение № 2
Критерии,
отвечающие условиям размещения постов радиационного контроля на промплощадке и
в СЗЗ ОИАЭ
1. Экологические критерии
Построение
систем контроля радиационной безопасности АС и других радиационно-опасных
предприятий атомной промышленности, как правило, базируется на какой-либо
концепции. В любой концепции построения такого рода систем лежит принцип
измерения параметров радиоактивного загрязнения, основанный на выборе датчиков,
измеряющих те или иные характеристики примеси - непосредственно ее концентрацию
(аспирационными датчиками [1])
или мощность дозы фотонного излучения [2],
количество датчиков и способ их размещения вокруг объекта. Продолжительность
периода осреднения уровней загрязнения определяет и способ размещения датчиков
вокруг АС - в направлении наиболее вероятных распространений выбросов.
Последние находим, исходя из розы ветров, составляемой по метеонаблюдениям в
течение года [3,
4].
Подобные системы хорошо себя зарекомендовали именно для анализа уровней
загрязнения при штатной работе АС, но, как отмечается в работах [1,
2,
5],
имеют существенный недостаток, поскольку вся информация о радиационной
обстановке относится к прошедшему времени, что совершенно недопустимо при
аварийных ситуациях. Следует также отметить, что сезонные розы ветров могут
отличаться от годовых, а потому наиболее вероятное направление распространения
выбросов с АС может меняться в пространстве и времени. Устранение последнего
недостатка, а также стремление восстановления
необходимой точности поля концентраций радиоактивных веществ в атмосфере и на
местности по показаниям датчиков, расположенных на местности, требует большого
количества датчиков, число которых растет с уменьшением погрешности
восстанавливаемого поля концентраций [6].
Например, если считать распределение концентрации радионуклида вблизи
поверхности земли в виде гауссовой функции ![]() , где qmax - значение концентрации в центре облака (x = 0, y
= 0), sу - дисперсия распределения, то для воспроизведения функции q(x,
y, t) с допустимой погрешностью d = 50 % необходимо иметь 70 точек
измерения, а при d = 30 %
- уже 200 точек [7].
Если учесть, что для каждого измерительного прибора необходимы линии связи,
обслуживание, т.е. специальный персонал, требующий, в свою очередь, социальных
затрат и т.д., нетрудно убедиться, что системы контроля, построенные по такому
принципу, достаточно дорогостоящи и малоэффективны в случае аварийных ситуаций,
т.к. не могут работать в режиме реального времени.
, где qmax - значение концентрации в центре облака (x = 0, y
= 0), sу - дисперсия распределения, то для воспроизведения функции q(x,
y, t) с допустимой погрешностью d = 50 % необходимо иметь 70 точек
измерения, а при d = 30 %
- уже 200 точек [7].
Если учесть, что для каждого измерительного прибора необходимы линии связи,
обслуживание, т.е. специальный персонал, требующий, в свою очередь, социальных
затрат и т.д., нетрудно убедиться, что системы контроля, построенные по такому
принципу, достаточно дорогостоящи и малоэффективны в случае аварийных ситуаций,
т.к. не могут работать в режиме реального времени.
2. Экономические критерии
С целью оптимального использования экспериментальных данных в последние годы была выдвинута идея сочетания измерительного и модельного мониторинга в единую систему таким образом, чтобы достоинства одного компенсировали недостатки другого [8]. Такого типа система должна обеспечивать непрерывный процесс адаптации модели распространения радиационного загрязнения среды к конкретным изменяющимся условиям по результатам фактических измерений на местности, что, в свою очередь, требует повышенной точности измерений. Повышение точности измерений возможно за счет снижения влияния внешнего и накапливающегося в точках контроля фона, исключения систематических ошибок, учета и автоматической компенсации нелинейности детекторов [9]. Важными факторами разработки систем являются экономические составляющие их создания и эксплуатации. Стоимость системы во многом определяется ценой комплектующих изделий, линий связи, монтажа и пусконаладочных работ. Повышение требований надежности, точности измерений (особенно в реальном масштабе времени), и быстродействия, расширение функций вместе с экономическими составляющими определяют требования и критерии при построении современных систем. Решение этих задач связано с определенными затратами, поэтому ведется поиск оптимального варианта их решения. Одним из наиболее важных параметров системы контроля является количество телеметрических систем, так как датчики, устанавливаемые на этих системах, дают непосредственно информацию о радиоактивном загрязнении окружающей среды и, кроме того, за счет своего количества, линий связи и необходимого технического обслуживания оказывают существенное влияние на стоимость системы в целом.
3. Физическо-технические критерии
Оценка радиоактивного загрязнения окружающей среды сводится к оценке загрязнения воздушного бассейна и подстилающей поверхности в направлении выброса, которые, в свою очередь, определяются величиной объемной активности радиоактивной примеси в воздухе, поверхностной активностью подстилающей поверхности при выпадении на нее радиоактивной примеси, а также мощностью дозы внешнего облучения и дозы при ингаляции в загрязненном районе. Если радионуклидный состав радиоактивной примеси известен хотя бы приблизительно (например, он может задаваться в рамках технологического регламента на АС или согласно критерию уровней аварии [7]), то использование датчиков мощности дозы внешнего облучения сети постов АСКРО, размещаемых на промплощадке АС, в СЗЗ и ЗН, позволяет уточнить величину мощности выброса и таким образом оценить масштабы радиоактивного загрязнения среды. Однако в этом случае к размещению датчиков АСКРО на промплощадке и в СЗЗ предъявляют определенные требования, заключающиеся в том, чтобы датчики располагались равномерно по азимуту, но на различных расстояниях от источника выбросов. Эти требования и определяют физические критерии, а также принцип размещения датчиков АСКРО в указанной области АС.
4. Демографический принцип размещения постов контроля АСКРО
При демографическом принципе размещения, фактически определенном Постановлением Правительства № 763 [10], посты ACKPO устанавливаются в крупных населенных пунктах в зоне наблюдения (ЗН) АС. Причем вопрос экономической целесообразности способа их размещения тесно связан с технической надежностью системы в целом. Анализ районов размещения АС (так называемых ситуационных планов) показывает, что такая сеть постов не может обеспечить надежную регистрацию аварийного выброса, поскольку при некоторых направлениях ветра его факел минует посты контроля. Повышение надежности за счет установки дополнительных постов приведет к резкому удорожанию АСКРО. К тому же, построенная по демографическому принципу, система способна только фиксировать ситуацию, тогда как на нее возлагаются еще и задачи прогнозирования распространения радиоактивного загрязнения, а также формирование обобщенной информации, необходимой для принятия решений о защите населения в случае аварии на АС. Единственным положительным моментом при подобном размещении постов АСКРО является социальная значимость системы оповещения - табло в населенных пунктах. Однако, используя традиционные средства связи, например местную радиотрансляционную сеть, такого же эффекта можно добиться значительно дешевле. Это означает, что демографический принцип размещения постов АСКРО в регионе АС не всегда пригоден и поэтому не может быть рекомендован для повсеместного применения.
5. Противоречия между экологическими и экономическими принципами размещения постов контроля АСКРО
Экологические и экономические принципы, следуя которым необходимо размещать датчики вокруг АС, вступают в явное противоречие. Решение проблемы достигается за счет использования принципа, так называемого гибридного мониторинга [8, 11-13], в котором данные математического прогнозирования корректируются с учетом показаний постов АСКРО. в России удалось найти оптимальное решение задачи с учетом экологических, экономических и демографических требований, предъявляемых к подобным системам [14]. На эту разработку был получен патент, закрепляющий приоритет России в этой области [15]. Оптимизация решения сводится к определению количества постов контроля (датчиков мощности дозы g - излучения), расположенных по правилу, согласно которому облако радиоактивной примеси, возникающее в результате аварии на АС, обязательно будет зарегистрировано хотя бы одним из них. Эта разработка получила поддержку в рамках международного сотрудничества при создании эскизного проекта, в частности, и для АСКРО Нововоронежской АС, что позволило в дальнейшем применить ее на Калининской, Балаковской и Ростовской АС.
Список литературы к Приложению № 2
1. Бондарев А.А., Дибобес М.К., Пюскюлян К.И. Об оценке радиационной обстановки в районе расположения АЭС при неконтролируемом поступлении радионуклидов во внешнюю среду. Атомная энергия т. 60, вып. 2, 1986, с. 138-139.
2. Лайхтман Д.Л., Мелкая И.Ю. О расчете турбулентных потоков по градиентным измерениям. Труды Ленинградского гидрометеорологического института. Некоторые вопросы физики пограничных слоев атмосферы и моря. 1970. Вып. 40, с. 64-73.
3. Седов Л.И. Методы размерности и подобия в механике. М.: Наука, 1987, 430 с.
4. Гост 8.361-79. Расход жидкости и газа. Методика выполнения измерений по скорости в одной точке сечения трубы. М.: Изд-во "Стандартов", 1985, 23 с.
5. Волков Э.П., Глущенко A.M., Дурнев В.Н. и др. О создании автоматизированных систем радиационного контроля внешней среды на АЭС. Атомная энергия, 1984, т.57, вып. I, с. 32-34.
6. Теверовский Е.Н., Дмитриев А.С., Кирдин Г.С. Автоматизированные системы прогнозирования и контроля загрязнения атмосферы при разовых выбросах из ЯЭУ, М.: Энергоатомиздат, 1983, 136 с.
7. Международная шкала ядерных событий (ИНЕС). Руководство для пользователей ИНЕС. - МАГАТЭ: Вена (Австрия), 1991.
8. Еремеев М.С., Еременко В.А., Жернов B.C. и др. Гибридный мониторинг радиационной обстановки перспективный подход к оперативному контролю и прогнозированию радиационных загрязнений среды выбросами и сбросами АЭС. - Атомная энергия, 1985, т. 59, вып. 5, с. 370-372.
9. Денисов А.А., Жернов В.С., Крашенинников М.С., Матвеев В.В., Рыжов Н.В., Скаткин В.М. Система радиационного контроля АЭС с распределенной структурой на микропроцессорах. Атомная Энергия, т. 53, вып. 3, 1982, с.131-138.
10. Постановление правительства РФ от 15.10.92 № 763. Система территориального радиационного контроля - СТРК.
11. Еремеев И.О., Шернов B.C., Клименко М.А., Коцарь Ю.Ю., Скаткин В.В. Цели и средства мониторинга радиоактивного загрязнения среды. Атомная энергия, т. 65, вып. 6, декабрь 1988, с. 437-439.
12. Хамьянов Л.П., Елохин А.П., Pay Д.Ф., Чистохин В.М. Автоматизированная система радиационного контроля на АЭС. Теплоэнергетика, 1989, Л12, с. 21-23.
13. Елохин А.П., Pay Д.Ф. О проблемах контроля радиационной обстановки в районах действующих АЭС. Энергия: экономика, техника, экология. 1996, с. 35-39.
14. Елохин А.П., Pay Д.Ф., Рыжов Н.В., Скаткин В.М., Халупкова Г.И. Концепция создания автоматизированной системы контроля радиационной обстановки в районе размещения атомных станций России. Тезисы докладов Международного симпозиума по радиационной безопасности. Москва, 1994, т. 1, с. 31.
15. Елохин А.П., Pay Д.Ф. Система контроля радиационной обстановки в зонах размещения объектов атомной промышленности. Патент РФ № 2042157, бюллетень № 23 от 20.08.95.
Приложение № 3
Методика обработки градиентных наблюдений
Существующие методики определения метеорологических параметров довольно сложны, поскольку требуют весьма точных измерений профиля скорости ветра, что возможно только на хорошо оборудованных метеостанциях. Рассматриваемая методика основана на нелинейной модели приземного слоя и является менее требовательной к точности градиентных наблюдений. Вычисления параметров проводят следующим образом [1]. Измеряют на двух уровнях скорость ветра и температуру, используя, как правило, значения z1=2 м и z2=0,5 м. Находят разность Dи=и(z1)-и(z2), Dq=q(z1)-q(z2).
Используя формулу ([2]) и выражения для скорости ветра и температуры через безразмерные величины (и=vиn/k, q=-qn/k, q0=P0/cpv*), получаем P0/cp=-kv*Dq/Dqn, Dи=v*Dиn/k.
![]() , (1)
, (1)
где иn, qn - табулированные значения универсальных функций, вычисленных для различных zn(zn=z/L), a Dиn, Dqn - их разность, k - постоянная Кармана. Поскольку Du, Dq - измеряемые величины, a Dиn, Dqn зависят от L, то выражение (1) есть неявная функция L. Для нахождения L задаются некоторым значением Lmax и варьируют его, например, Li=DLi, i = 1, 2, 3, _ N, DL=Lmax/N до тех пор, пока разность или относительная погрешность
 ,
,  (2)
(2)
не
будет минимальной (в пределе e = 0). Найденное значение L*, при
котором e минимальна, и определит искомое значение
L: L=DLi*. Определив L и пересчитав zn при фиксированных z1 и z2, т.е., таким образом, пересчитав Dqn, Dиn, найдем ![]()
![]() (3)
(3)
или
![]() . (4)
. (4)
При
стремлении ![]() ,
, ![]() . Подобный
метод расчета наиболее целесообразен при расчете метеопараметров на ЭВМ.
Поскольку параметр L может быть как L > 0, так и L <
0 (при L = 0 режим движения теряет турбулентный характер ([1],
стр. 74)), то всевозможные вариации Li должны проводиться по формуле: Li=DL(N+L-i), i = 1, 2, 3, ..., N, N
+ 1, N + 2, ..., 2N + 1. Последнее позволит учесть различную
стратификацию слоя атмосферы, задаваемую температурным режимом. Для расчета иn(zn), kn(zn) при найденном L целесообразно
пользоваться не таблицами, а аналитическим значением y как функцией zn [2].
Выбор иn,
qn по заданному zn осуществляется следующим образом при
известном zn
находят у, по которому из таблицы находят значения соответствующие иn или qn. Аналогично находят значения для другого
значения zn
(другого уровня), вычисляя затем разности Dиn, Dqn. После определения параметров L, v* значения u(z), k(z) находят по формулам (9),
(10) Приложения № 4.
Постоянную с1 в [2]
находят при z=z0 и и(z)½z=z0=0.
. Подобный
метод расчета наиболее целесообразен при расчете метеопараметров на ЭВМ.
Поскольку параметр L может быть как L > 0, так и L <
0 (при L = 0 режим движения теряет турбулентный характер ([1],
стр. 74)), то всевозможные вариации Li должны проводиться по формуле: Li=DL(N+L-i), i = 1, 2, 3, ..., N, N
+ 1, N + 2, ..., 2N + 1. Последнее позволит учесть различную
стратификацию слоя атмосферы, задаваемую температурным режимом. Для расчета иn(zn), kn(zn) при найденном L целесообразно
пользоваться не таблицами, а аналитическим значением y как функцией zn [2].
Выбор иn,
qn по заданному zn осуществляется следующим образом при
известном zn
находят у, по которому из таблицы находят значения соответствующие иn или qn. Аналогично находят значения для другого
значения zn
(другого уровня), вычисляя затем разности Dиn, Dqn. После определения параметров L, v* значения u(z), k(z) находят по формулам (9),
(10) Приложения № 4.
Постоянную с1 в [2]
находят при z=z0 и и(z)½z=z0=0.

Рис. 1. Зависимость скорости приземного ветра U(z) от высоты от подстилающей поверхности (модель приземного слоя атмосферы): 1 - неустойчивое состояние (L=-18. v*= 0,32 м/с), 2 - устойчивое состояние (L =30, v* = 0,26 м/с)
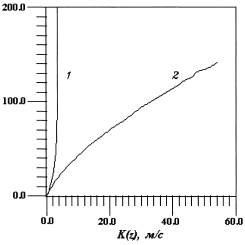
Рис. 2. Зависимость коэффициента турбулентной диффузии K(z) от высоты от подстилающей поверхности при различных состояниях устойчивости атмосферы: 1 -неустойчивое состояние (L =-181), 2 -устойчивое состояние (L= 30)
Рассчитанные значения u(z), k(z) для двух случаев - L > 0, L < 0 приводятся в виде графиков на рис. 1, 2.
Следует отметить, что для применения методики градиентных наблюдений над скоростью ветра и температурой можно использовать не только стандартные, но и любые другие уровни, на которых размещаются датчики для измерения метеопараметров [3, 4]. Более того, в условиях, когда уровень шероховатости подстилающей поверхности нельзя считать однородным на достаточно протяженной области X~1,5-2,0 км, для наблюдения метеопараметров целесообразно выбирать уровни размещения датчиков не ниже 20 м [5].
Список литературы к Приложению № 3
1. Лайхтман Д.Л. Физика пограничного слоя атмосферы. Л.: Гидромет. изд-во, 1970, 340 с.
2. Елохин А.П. Оптимизация методов и средств автоматизированных систем контроля радиационной обстановки окружающей среды. Диссертация на соискание ученой степени доктора технических наук. М.: МИФИ, 2001, 325 с.
3. Зилитинкевич С.С. Динамика пограничного слоя атмосферы. Л.: Гидрометиздат, 1970, 296 с.
4. Зилитинкевич С.С., Чаликов Д.В. Определение универсальных профилей скорости ветра и температуры в приземном слое атмосферы. Изв. АН СССР, сер. "Физика атмосферы и океана", №. 4, № 3, 1968.
5. Елохин А.П., Холодов Е.А., Жилина М.В. Влияние изменения шероховатости подстилающей поверхности на формирование следа при ее радиоактивном загрязнении. Метеорология и гидрология, № 5, 2008, с. 69-80.
Приложение № 4
Модель пограничного слоя атмосферы
Турбулизованный под влиянием подстилающей поверхности слой называется планетарным пограничным слоем атмосферы. Его толщина зависит от скорости внешнего потока (потока на большое расстояние от земной поверхности - в свободной атмосфере), от вертикальной стратификации, от размеров и формы неровностей подстилающей поверхности. Пограничный слой атмосферы характеризуется не только непрерывным ростом скорости от нуля до величины, соответствующей потоку в свободной атмосфере, но и вполне закономерным изменением направления ветра при всех вращениях. Последнее обусловлено влиянием силы Кориолиса (fк). Механизм правого вращения ветра становится понятным, если руководствоваться следующими соображениями.
Вблизи земной поверхности градиент давления уравновешивается силой трения (fтр). С увеличением высоты и уменьшением затормаживающего влияния земной поверхности уменьшается сила трения, растет скорость, а пропорционально возрастанию скорости увеличивается fк, пропорционально которой и увеличивается изменение направления ветра. Динамическое влияние земной поверхности, как указывают опытные данные, проявляется до высоты 1,5-2 км, что справедливо и для монотонного правого вращения ветра (угол поворота на этой высоте может достигать 24°). Дальнейшие изменения направления уже невелики и теряют монотонный характер. Рассматривая задачу формирования метеопараметров в пограничном слое атмосферы, ограничимся случаем стационарности и однородности вдоль оси [1]. Система уравнений, описывающих пограничный слой, состоит из уравнений, описывающих вертикальные профили турбулентных напряжений (уравнений динамики) при и=v*иn/k и v= v*vn/k
 , (1)
, (1)
![]() ,
, ![]() , k -
постоянная Кармана;
, k -
постоянная Кармана;
u - продольная скорость ветра;
![]() - поперечная скорость ветра, соответственно;
- поперечная скорость ветра, соответственно;
![]() - продольное турбулентное напряжение;
- продольное турбулентное напряжение;
![]() - поперечное турбулентное напряжение.
- поперечное турбулентное напряжение.
Уравнение для коэффициента турбулентности:
![]() (2)
(2)
Уравнение баланса энергии турбулентной пульсации:
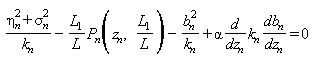 , (3)
, (3)
где
![]() ,
, ![]() , С -
численный коэффициент, определяемый эмпирически.
, С -
численный коэффициент, определяемый эмпирически.
Уравнения для масштаба турбулентных пульсаций:
 (4)
(4)
Уравнение для потока тепла:
![]() , (5)
, (5)
где L - масштаб Монина-Обухова, v* - динамическая скорость, определяемые по данным наблюдения в приземном слое, Hn - безразмерная высота пограничного слоя, получаемая из уравнения:
![]() , (6)
, (6)
где e2 - малая величина (e2 = 0,05).
Уравнения (1) - (6) дополняются граничными условиями:
при ![]() :
: ![]() ,
, ![]() ;
; ![]() ,
, ![]() ; (7)
; (7)
при ![]() :
: ![]() ,
, ![]() ;
; ![]() . (8)
. (8)
В представленной форме система содержит лишь параметр m0=L1/L. Численное значение величины a2 можно варьировать, учитывая, таким образом, различие профилей лучистого притока тепла. При расчетах задают величину a2/Hт, а по найденному значению Hn из (6) находят a2. При расчетах полагали ab=0,73, C = 0,046, k = 0,4, a = 0,54. Характерная зависимость высоты пограничного слоя атмосферы от состояния ее устойчивости (параметра m0) приведена на рис. 1.
Решение системы (1) - (8) находили численно с итерациями по kn следующим образом:
1. Задание kn в виде линейной зависимости от zn(kn= zn).
2. Решение системы (1) при заданном kn (методом матричной прогонки).
3. Решение уравнения (6) (методом Ньютона).
4. Определение ln из (4).
5. Вычисление нового значения, согласно (2).
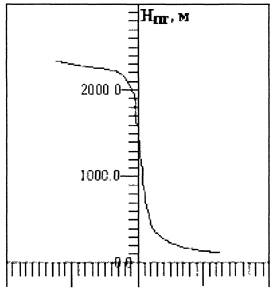
Рис. 1. Зависимость высоты пограничного слоя атмосферы от состояния ее устойчивости, характеризуемой параметрам m0.
Этот цикл повторяется до тех пор, пока çki+1-kiç не становится малой величиной (i - номер итерации). После чего анализируют, при каком значении zn выполняется условие (6). Это значение и принимается за безразмерное значение высоты пограничного слоя, а H=L1Hn. После решения системы искомые величины u(z), v(z), k(z), b(z) находят по формулам:
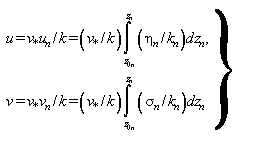 ; (9)
; (9)
![]() ; (10)
; (10)
![]() . (11)
. (11)
Характерные зависимости продольной и поперечной скоростей ветра как функции высоты приведены на рис. 2, 3.
При определенных параметрах u(z), v(z) и k(z) уравнения турбулентной диффузии (13)-(15) Приложения № 16 формулируют следующим образом: предполагают, что размывание примеси по оси Y осуществляется по закону Гаусса, определяя, таким образом, концентрацию примеси выражением [2]:
 , (12)
, (12)
где sу(х) - среднеквадратичное отклонение. Интегрируя уравнение турбулентной диффузии (13) Приложения № 16, согласно (13),
 (13)
(13)
и, используя (12), получают:
 , (14)
, (14)
где
S = S(x, z, t);  ; hэф - эффективная высота выброса; Pв - мощность выброса, [Бк/с]; f=PBd(x)d(y)d(z-hэф) - источник радиоактивной примеси; w - скорость
гравитационного осаждения примеси; s - постоянная релаксации примеси за счет
ее радиоактивного распада или вымывания из атмосферы.
; hэф - эффективная высота выброса; Pв - мощность выброса, [Бк/с]; f=PBd(x)d(y)d(z-hэф) - источник радиоактивной примеси; w - скорость
гравитационного осаждения примеси; s - постоянная релаксации примеси за счет
ее радиоактивного распада или вымывания из атмосферы.

Рис. 2. Зависимость продольной составляющей скорости ветр a U(z) от высоты при различном состоянии устойчивости атмосферы (1-7) в модели пограничного слоя атмосферы

Рис. 3. Зависимость поперечной составляющей скорости ветра V(z) от высоты при различных состояниях устойчивости атмосферы (1-7) в модели пограничного слоя атмосферы
В
рамках модели пограничного слоя атмосферы [2],
![]() , где
, где ![]() - усредненные по пограничному слою значения:
энергии турбулентных пульсаций b(х), коэффициента турбулентной диффузии k(х),
продольной скорости ветра u(х). Обрабатывая граничные и начальные
условия аналогично уравнению (15) Приложения
№ 16, получают:
- усредненные по пограничному слою значения:
энергии турбулентных пульсаций b(х), коэффициента турбулентной диффузии k(х),
продольной скорости ветра u(х). Обрабатывая граничные и начальные
условия аналогично уравнению (15) Приложения
№ 16, получают:
![]() , (15)
, (15)
 ,
,
где b - скорость сухого осаждения примеси; z0 - параметр шероховатости.
Список литературы к Приложению № 4
1. Бобылева М.М. Расчет характеристик турбулентности в планетарном пограничном слое атмосферы. Труды Ленинградского Гидрометеорологического института. Вып. 40 (Некоторые вопросы физики пограничного слоя в атмосфере и море). Л., 1970.
2. Лайхтман Д.Л. Физика пограничного слоя атмосферы. Л.: Гидромет. изд-во, 1970, 340 с.
Приложение № 5
Скорость сухого осаждения
Скорость сухого осаждения - это отношение интенсивности оседания примеси в Бк/м2 к концентрации в приземном слое воздуха в Бк/м3. Скорость сухого осаждения определяется силой тяжести и зависит от аэродинамического размера частиц. Для частиц диаметром от 0,1 до 1 мкм скорость сухого осаждения равна 0,02 см/с, для частиц диаметром от 1 до 10 мкм она изменяется от 0,02 до 5 см/с. Эта величина зависит также от типа поверхности и физико-химических свойств радионуклида [1].
Значения скорости сухого осаждения для различных нуклидов и типов поверхности приведены в таблице.
|
Нуклид |
Скорость осаждения, см/с |
Источник информации |
|||
|
Вода |
Почва |
Трава |
Липкая бумага |
||
|
Цезий-137 |
0,9 |
0,04 |
0,2 |
0,2 |
[1] |
|
Рутений-103 |
2,3 |
0,4 |
0,6 |
0,4 |
|
|
Цирконий-95, Ниобий-95 |
5,7 |
2,9 |
- |
1,4 |
|
|
Церий-141 |
- |
- |
- |
0,7 |
|
|
Теллур-127 |
- |
- |
- |
0,7 |
|
|
Элементарный йод |
- |
1,0 |
- |
- |
[2] |
|
Органические соединения йода |
- |
0,01 |
- |
- |
|
|
Аэрозоли |
- |
0,8 |
- |
- |
|
|
Инертные радиоактивные газы |
- |
0 |
- |
- |
|
Список литературы к Приложению № 5
1. Сахаров В.К. Радиоэкология: Учебное пособие. СПб.: Издательство "Лань", 2006, 320 с.
2. Пути миграции искусственных радионуклидов в окружающей среде. Радиоэкология после Чернобыля. Под ред. Ф. Уорнера, Р. Харрисона. М.: Мир, 1999.
3. Гусев Н.Г., Беляев В.А. Радиоактивные выбросы в биосфере. Справочник. М.: Энергоатомиздат 1986, 224 с.
Приложение № 6
Шероховатость подстилающей поверхности
|
Тип поверхности |
z0, см |
|
Очень гладкая (грязевое болото, лед) |
0,001 |
|
Гладкий снег на невысокой траве |
0,005 |
|
Песок |
0,1-0,05 |
|
Ровный мощный снежный покров, нивелирующий все особенности подстилающей поверхности |
0,2-0,10 |
|
Пустыня |
0,03 |
|
Естественная снежная поверхность |
0,1-0,5 |
|
Слабый рыхлый снег, неровный снежный покров |
0,5-2,0 |
|
Газон с травой высотой до 1 см |
0,1 |
|
Ровная обнаженная площадка или площадка с низким травяным покровом |
0,3-1,0 |
|
Паровое поле |
0,5-2,0 |
|
Равнина, редкая трава высотой до 10 см |
0,6-0,7 |
|
Скошенная трава высотой: |
|
|
1,5 см |
0,2 |
|
3,5 см |
0,5-0,7 |
|
4,5 см u 2 м = 2 м/сек |
2,4 |
|
u 2 м = 6-8 м/сек |
1,7 |
|
Равнина с невысокой густой травой высотой до 5 см, степь |
2-3 |
|
Полупустыня с отдельными кустиками ксерофитов высотой до 30 см |
3-4 |
|
Пшеничное поле |
3-7 |
|
Картофельное поле |
4-7 |
|
Свекольное поле |
6,0-6,5 |
|
Равнина с редкой травой высотой до 50 см |
5 |
|
Равнина с густой травой высотой до 50 см |
9-10 |
|
Равнина с высокой травой (60-70 см): |
|
|
u 2 м = 1,5 м/сек |
9,0 |
|
u 2 м = 3,3 м/сек |
6,1 |
|
u 2м = 6,2 м/сек |
3,7 |
|
Открытые деревья |
1,0 |
|
Двухэтажные здания |
10 |
|
Городская застройка |
40-80 |
Приложение № 7
Постоянная вымывания осадками радиоактивной примеси
Вымывание является важным процессом удаления радионуклидов из атмосферы [1]. Процесс вымывания примесей из атмосферы разделяют на две стадии. В первой стадии вещество, которое вымывается или принимает участие в образовании капли облака и является ядром конденсации, или захватывается каплями облаков на этапе их развития, когда они еще не превратились в падающие дождевые капли. Эта стадия определяется как внутриоблачное вымывание. Во второй стадии вещество захватывает капля падающего дождя на всем пути полета до контакта с подстилающей поверхностью. Это стадия подоблачного вымывания. Существуют пять механизмов вовлечения молекул газа или частиц в каплю: 1) диффузофорез; 2) броуновская диффузия; 3) соударение и захватывание; 4) растворение газа; 5) образование капель на ядрах конденсации. Во время диффузофореза аэрозольные частицы движутся в направлении среднего потока молекул в воздухе. Явление диффузофореза характерно лишь для частиц диаметром менее 0,1 мкм. Общий вклад такого механизма в вымывание частиц дождевыми каплями незначителен. Случайное перемещение мелких частиц, вызванное столкновением с молекулами газа, также может способствовать переносу частицы к поверхности капли. Скорость броуновской диффузии определяется преимущественно размером частиц, и ее влияние становится ощутимым для частиц диаметром менее 0,1 мкм. В отличие от диффузии частиц, диффузия молекул газа является главным механизмом их перемещения к поверхности капли. Механизм инерционного соударения и захватывания характерен лишь для подоблачного вымывания. Молекулы газа благодаря своей легкости обходят падающую каплю, в то время как частицы со значительно большей массой оказывают сопротивление изменениям движения. Чем массивнее частица, тем в меньшей степени она претерпевает такие изменения.
Коэффициент
вымывания зависит от интенсивности дождя [2].
Этот вопрос наиболее полно
освещен в [3],
[4].
Вместе с тем известно, что снегопад лучше очищает атмосферу, чем дождь. Так при
испытаниях ядерного оружия коэффициент вымывания снегом давал значения в
несколько раз превышающие значения для дождя (![]() , [3])
, [3])
На
вымывание газов дождями сильное влияние оказывает их растворимость в воде. Если
объемная растворимость сернистого газа в воде при 0 °С составляет 79,8 (![]() - величина,
сравнимая с коэффициентом вымывания атмосферной пыли), то радона - 0,51.
Располагая газы, входящие в состав земной атмосферы, в порядке их растворимости,
получают следующий ряд, где растворимость убывает от 1,71 до 0,012:
- величина,
сравнимая с коэффициентом вымывания атмосферной пыли), то радона - 0,51.
Располагая газы, входящие в состав земной атмосферы, в порядке их растворимости,
получают следующий ряд, где растворимость убывает от 1,71 до 0,012: ![]() . Таким
образом, практически все газы, за исключением двуокиси углерода CO2 и двуокиси азота NO2, вымываются хуже радона, а значит хуже аэрозолей не менее
чем на порядок [3].
. Таким
образом, практически все газы, за исключением двуокиси углерода CO2 и двуокиси азота NO2, вымываются хуже радона, а значит хуже аэрозолей не менее
чем на порядок [3].

Рис. 1 Коэффициенты вымывания частиц единичной плотности из подоблачного слоя атмосферы в зависимости от интенсивности дождя I для различных значений а2р (Chamberlain, 1953.) [4]: 1-4 мкм2 г/см3; 2-7,8 мкм2 г/см3; 3-16 мкм2 г/ см3; 4-41 мкм2 г/см3; 5-81 мкм2 г/см3; 6-169 мкм2 г/см3; 7-400 мкм2 г/см3.
Зависимость
коэффициента вымывания аэрозолей от размера капель дождя рассмотрена в работе [4].
Там же показано, что время жизни частицы t, сек-1 (время, в течение
которого концентрация частиц золя уменьшается в e раз) выражается через
характерный параметр дождя - интенсивность I (г/см2 ×сек) формулой ![]() , где Rm - наиболее часто встречающийся радиус
водяных капель, K - коэффициент захвата. Представляя постоянную
вымывания в виде 1/t,
находим
, где Rm - наиболее часто встречающийся радиус
водяных капель, K - коэффициент захвата. Представляя постоянную
вымывания в виде 1/t,
находим ![]() , т.е.
постоянная вымывания линейно зависит от интенсивности осадков.
, т.е.
постоянная вымывания линейно зависит от интенсивности осадков.
Более общая зависимость представлена в виде графика на рис. 1 [3], из которой с определенной погрешностью можно принять зависимость постоянной вымывания от интенсивности осадков линейной. Дальнейший анализ показывает, что для мелких частиц справедлива линейная зависимость коэффициента вымывания от интенсивности дождя, а для крупных эта зависимость отличается от линейной. Из работ Мейсона, Кинцера и Кобба также следует, что коэффициент вымывания для крупных частиц есть степенная функция от интенсивности дождя с показателем степени от 0,75 до 0,8, однако существует значительный разброс этих значений как в пределах ливня, так и между разными ливнями [3]. В практических целях рекомендуется использовать значения постоянной вымывания, приведенные в таблице 1 [5].
Постоянную
вымывания также можно представить в виде ![]() , где I
- интенсивность осадков, мм/ч; ky - величина абсолютной вымывающей
способности дождя (для всех нуклидов, за исключением инертных газов, ky=10-5 ч/(мм×с)), характерная для дождя интенсивностью
I = 1 мм/ч, k0 - относительная вымывающая способность
осадков других типов. Относительная вымывающая способность различных типов
осадков приведена в таблице 2
[4].
, где I
- интенсивность осадков, мм/ч; ky - величина абсолютной вымывающей
способности дождя (для всех нуклидов, за исключением инертных газов, ky=10-5 ч/(мм×с)), характерная для дождя интенсивностью
I = 1 мм/ч, k0 - относительная вымывающая способность
осадков других типов. Относительная вымывающая способность различных типов
осадков приведена в таблице 2
[4].
|
Форма нуклида |
Постоянная вымывания Ламбда, 1/с |
|
Элементарный йод |
1,3´10(-4) |
|
Органические соединения йода |
1,3´10(-6) |
|
Аэрозоли |
2,6´10(-5) |
|
Газы |
0 |
|
Тип осадков |
k0 |
|
Дождь |
1,0 |
|
Дождь с грозой |
1,1 |
|
Снег с дождем |
2,4 |
|
Ливень |
2,8 |
|
Снег |
3,0 |
|
Морось |
4,5 |
|
Туман |
5,0 |
Список литературы к Приложению № 7
1. Пути миграции искусственных радионуклидов в окружающей среде. Радиоэкология после Чернобыля. Под ред. Ф. Уорнера, Р. Харрисона. М.: Мир, 1999.
2. Гаргер Е.К., Гаврилов В.П., Жуков Г.П., Самарская Н.А. Лагранжева модель регионального переноса и рассеяния полидисперсной примеси в нижних слоях тропосферы. Труды ИЭМ, 1986, вып. 14(129), с. 20-30.
3. Метеорология и атомная энергия. Под ред. Н.Л. Бызовой. Л.: Гидрометеоиздат, 1971, 648 с.
4. Бютнер Э.К., Гисина Ф.А. Эффективный коэффициент захвата частиц аэрозоля дождевыми и облачными каплями. Труды ЛГМИ, вып. 15, с. 103-117.
5. Гусев Н.Г., Беляев В.А. Радиоактивные выбросы в биосфере. Справочник. М.: Энергоатомиздат 1986, 224 с.
Приложение № 8
Постоянная распада радиоактивной примеси
При нормальной эксплуатации реакторов
радиационная обстановка в районе размещения АС формируется в основном выбросами
инертных радиоактивных газов (ИРГ )(изотопов Ar, Kr, Xe), 131I и другими продуктами деления (89Sr, 90Sr, 134Cs, 137Cs), а также продуктов коррозии (58Co, 60Co, 51Cr, 54Mn и т.д.). Для реакторов на быстрых
нейтронах с натриевым теплоносителем основными источниками загрязнения
окружающей среды являются 22Na, 24Na и 41Ar. В действительности спектр
радионуклидов, выбрасываемых в атмосферу реакторами и другими предприятиями
топливного цикла, очень широк и разнообразен. Поэтому в каждом конкретном
случае требуется детальное экспериментальное исследование. В таблице приведены
характеристики основных радионуклидов, выбрасываемых в атмосферу АС и другими
ОИАЭ [1,
2].
Постоянная распада для радионуклида определяется по формуле: ![]() , где T1/2 - период полураспада радионуклида.
, где T1/2 - период полураспада радионуклида.
|
Радионуклид |
T1/2 |
Энергия фотонного излучения Е __гамма, МэВ |
Квантовый выход на 100 распадов эта, % |
|
(133)Xe |
5,247 сут. |
0,081 |
37,4 |
|
(135)Xe |
9,10 ч |
0,25 |
90,1 |
|
(135m)Xe |
15,29 мин |
0,527 |
80,7 |
|
(137)Xe |
3,82 мин |
0,456 |
30,0 |
|
(138)Xe |
14,08 мин |
0,258 |
31,5 |
|
0,435 |
20,2 |
||
|
1,768 |
16,7 |
||
|
(85m) Кг |
4,48 ч |
0,151 |
75,5 |
|
0,305 |
14,0 |
||
|
(87) Кг |
76,31 мин |
0,403 |
48,3 |
|
0,846 |
7,25 |
||
|
2,555 |
13,0 |
||
|
(88) Кг |
2,84 ч |
0,196 |
37,8 |
|
0,830 |
13,0 |
||
|
2,392 |
37,8 |
||
|
(89) Кг |
3,15 мин |
0,22 |
22,5 |
|
0,586 |
24,9 |
||
|
(41)Ar |
1,84 ч |
1,294 |
99,2 |
|
(131)I |
8,04 сут. |
0,364 |
82,4 |
|
(134)Cs |
2,062 г. |
0,796 |
85,1 |
|
0,605 |
97,5 |
||
|
0,569 |
15,0 |
||
|
(137)Cs |
30,174 г. |
0,661 |
85,1 |
|
(54) М№ |
312,39 сут. |
0,835 |
99,98 |
|
(60)Co |
5,272 г. |
1,333 |
99,98 |
|
1,173 |
99,87 |
||
|
(51)Cr |
27,73 сут. |
0,320 |
9,83 |
|
(95)Zr |
64,05 сут. |
0,757 |
55,4 |
|
0,724 |
43,7 |
||
|
(95)№b |
34,97 сут. |
0,766 |
99,8 |
|
(99)Mo |
66,02 ч |
0,739 |
12,8 |
|
0,181 |
6,35 |
||
|
0,141 |
89,6 |
||
|
(103)Ru |
39,35 сут. |
0,497 |
90,0 |
|
0,610 |
5,85 |
||
|
(106)Ru |
368 сут. |
0,622 |
9,94 |
|
0,512 |
20,6 |
||
|
(110m)Ag |
250,4 сут. |
0,938 |
32,4 |
|
0,885 |
76,4 |
||
|
0,658 |
94,2 |
||
|
(125)Sb |
2,77 г. |
0,636 |
11,2 |
|
0,601 |
18,4 |
||
|
0,428 |
29,6 |
||
|
(132)Te |
78,2 ч |
0,228 |
85,0 |
|
(140m)Ba |
12,789 дней |
0,537 |
23,8 |
|
0,163 |
5,95 |
||
|
(140)La |
40,22 ч |
1,596 |
95,47 |
|
0,816 |
22,52 |
||
|
0,487 |
43,43 |
||
|
(141)Ce |
32,50 дней |
0,145 |
49,0 |
|
(144)Ce |
284,31 дней |
0,134 |
10,8 |
|
(237)U |
6,75 дней |
0,208 |
22,4 |
|
0,059 |
34,6 |
||
|
(154)Eu |
8,5 г. |
1,274 |
35,5 |
|
0,722 |
19,7 |
||
|
0,123 |
40,5 |
||
|
(58)Co |
70,78 дней |
0,811 |
99,45 |
|
(22)№a |
2,602 г. |
1,275 |
99,95 |
|
(24)№a |
15,01 ч |
2,754 |
99,87 |
|
1,369 |
99,99 |
Список литературы к Приложению № 8
1. Гусев Н.Г., Дмитриев П.П. Квантовое излучение радиоактивных нуклидов. Справочник. М.: Атомиздат, 1977, 395 с.
2. Гусев Н.Г., Беляев В.А. Радиоактивные выбросы в биосфере. Справочник. М.: Энергоатомиздат 1986, 224 с.
Приложение № 9
Скорость гравитационного осаждения
Значения скорости гравитационного осаждения Wg [м/с] для частицы плотностью v [г/см3] c диаметром d [см] определяются по формулам Стокса:
![]() ,
,  ;
;
![]() ,
, 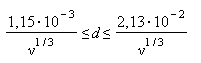 .
.
Скорость гравитационного осаждения изменяется от 0,001 до 0,2 м/с.
Приложение № 10
Рекомендации к датчикам метеопараметров
Задание
разностей скоростей ветра и температуры предъявляет особое требование к
точности приборов, определяющих эти параметры. Для анеморумбографа - прибора,
измеряющего скорость ветра, погрешность определяется выражением: ![]() , где
, где ![]() - усредненное значение скорости ветра,
измеренной на уровне z в течение определенного промежутка времени Dt ~ 10 мин. Для
определенных таким образом погрешностей скоростей ветра
- усредненное значение скорости ветра,
измеренной на уровне z в течение определенного промежутка времени Dt ~ 10 мин. Для
определенных таким образом погрешностей скоростей ветра ![]() ,
, ![]() , измеряемых
на уровнях z1,
z2,
погрешность разности определится выражением, [1]:
, измеряемых
на уровнях z1,
z2,
погрешность разности определится выражением, [1]:
![]() .
.
При
минимально возможной измеряемой скорости vmin= 1,2 м/с погрешность составляет 0,483 м/с.
Если погрешность датчика, используемого для измерения температуры есть ![]() , то
погрешность разности температур (
, то
погрешность разности температур (![]() ),
измеряемых на уровнях z1,
z2,
определим аналогично:
),
измеряемых на уровнях z1,
z2,
определим аналогично:
![]() .
.
При изменении температуры от 253°К (-20 °С) до 298°К (+25 °С) погрешность измерения составляет от 2,85° до 3,24°. Таким образом, для повышения точности определения параметров L, v*, u(z), k(z) необходимо уменьшить погрешность определения скоростей ветра и температуры или сконструировать датчики, измеряющие непосредственно разность этих параметров.
Другие методы, позволяющие уменьшить погрешность оценки высотных распределений скорости ветра и температуры, - это методы, сводящиеся к нормировке полученных расчетных распределений на показание датчика, расположенного на определенной высоте (уровне h ~ 30 - 40 м) на метеомачте [2, 3]. Результаты сравнения скорректированных таким образом расчетных распределений скорости ветра с экспериментальными данными, полученными на высотных метеомачтах при различных состояниях устойчивости атмосферы, показывают, что такого рода корректировка высотных распределений метеопараметров позволяет существенно повысить точность прогностических оценок уровней радиоактивного загрязнения подстилающей поверхности в условиях радиационных аварий.
Список литературы к Приложению № 10
1. Тэйлор Дж. Введение в теорию ошибок. М.: Мир, 1985, 272 с.
2. Елохин А.П. Оптимизация методов и средств автоматизированных систем контроля радиационной обстановки окружающей среды. Диссертация на соискание ученой степени доктора технических наук. - МИФИ. 2001. 325 с.
3. Елохин А.П. Выбор оптимальной высоты метеомачты для задач прогнозирования радиоактивного загрязнения окружающей среды при выбросах АЭС. Научная сессия МИФИ-99. Сборник научных трудов, Москва, 1999, Январь 18-22, т. 1, с.31-32.
Приложение № 11
ПС "RECASS"
Компьютерная система "RECASS" предназначена для поддержки принятия решений в задачах радиоэкологического анализа и прогностических оценок радиоактивного загрязнения окружающей среды при радиационных авариях [1, 2]. Организацией-разработчиком ПС "RECASS" является НПО "Тайфун". ПС "RECASS" получило широкое распространение на ряде Российских АС, используется при проведении учений на АС, организуемых эксплуатирующей организацией, но в настоящий момент еще не аттестовано, что сдерживает его распространение.
Основу программного средства (ПС), построенного по модульному принципу, составляет модули STAMP и RIMPUFF.
Программная реализация модулей STAMP и RIMPUFF выполнена в рамках единой технологии ПС "RECASS" и входит в банк моделей системы "RECASS", объединяющий в настоящее время модели, выполненные на разной методической основе, различного пространственного разрешения и, соответственно, разной оперативности.
В модуле STAMP проведена программная реализация моделей атмосферной диффузии и расчета доз облучения по стандартным методикам (методика МАГАТЭ [3], приведенная в Приложении № 17, методика МХО "Интератомэнерго" [4, 5-7] и методические указания Минатома России [8]).
В модуле RIMPUFF выполнена программная реализация мезомасштабной модели атмосферной диффузии, разработанной в национальной лаборатории RISO, Дания.
Мезомасштабная модель атмосферной диффузии RIMPUFF предназначена для прогноза распространения загрязненной примеси при выбросах от одного или нескольких источников переменной мощности.
Модель позволяет учитывать нестационарность и пространственную изменчивость поля ветра и состояний устойчивости атмосферы в условиях сложного рельефа и применяется для восстановления картины загрязнения на расстоянии до 50 км от места выброса. Распространение примеси моделируется серией клубов, имеющих Гауссову форму во всех трех измерениях и перемещающихся в поле ветра.
Результатом работы модели является в общем случае пространственно-временной набор полей значений мгновенных или интегральных концентраций примеси в воздухе и на подстилающей поверхности.
Как известно, общим недостатком стандартных моделей Гауссовой струи является невозможность их применения при реальных нестационарных и неоднородных атмосферных ситуациях. Погрешность их результатов прогрессирует с изменением расстояния. Радиус действия ограничивается несколькими десятками километров. Стандартное моделирование диффузии при неоднородных и нестационарных условиях ограничивается множественностью характеристик потоков, имеющих место при таких условиях.
Модель RIMPUFF, по мнению разработчиков ПС, решает эти проблемы, вызванные большим количеством характеристик атмосферных потоков, моделируя струю множеством отдельных клубов, самостоятельно передвигающихся в поле меняющегося ветра.
На каждом временном шаге модель рассчитывает перенос, диффузию и осаждение индивидуальных клубов в соответствии с локальными метеорологическими условиями. Общее поле загрязнения строится как суперпозиция концентраций отдельных клубов и хранится в равномерной сетке заданного разрешения.
Модель в состоянии одновременно отслеживать до 32000 индивидуальных клубов, что значительно превышает количество, необходимое для решения большинства прикладных задач.
Распределение концентрации индивидуального клуба предполагается Гауссовым во всех трех пространственных измерениях. Размер каждого клуба характеризуется стандартным отклонением (дисперсией), зависящим от устойчивости атмосферы, высоты центра клуба и пройденного расстояния.
Со временем размер отдельного клуба может достичь довольно большого значения, что будет приводить к усреднению характеристик и сглаживанию детальности входной информации. Для избежания этого предусмотрен механизм разделения клуба на пять более мелких (с сохранением массы) при достижении им определенного размера. В качестве этого критического размера клуба принимается половина длины диагонали ячейки сетки ветра, при этом такой размер не должен превышать двух диагоналей ячейки сетки концентраций.
Высота центра масс клуба определяется высотой выброса и тепловым подъемом клуба, который рассчитывается, исходя из характеристик источника и локальных атмосферных характеристик, и ограничивается высотой пограничного слоя атмосферы.
Учитывается сухое и влажное осаждение примеси, а также радиоактивный распад вещества.
Указанный выше подход к моделированию атмосферной диффузии примеси позволил разделить расчет выпадений радиоактивных веществ и концентраций их в воздухе на две независимые части [2]:
перенос клубов в пространстве (эволюцию) с одновременной коррекцией их характеристик;
расчет выпадений и концентраций в воздухе радиоактивных веществ путем суперпозиции выпадений и концентраций в воздухе от каждого клуба.
Поскольку инциденты, приводящие к выбросу радиоактивных веществ в атмосферу, могут иметь достаточно разнообразные характеристики, то с целью унификации программной реализации модели было принято решение разделить первую часть задачи на два независимых блока:
генерация клубов по описанию сценария развития инцидента;
перенос сформированных клубов в соответствии с метеорологическими условиями и характеристиками местности.
Таким образом, окончательный вариант программной реализации модели мезомасштабного переноса радиоактивных веществ в случае аварии на радиационно-опасных объектах содержит следующие программные модули:
программа генерации клубов с радиоактивными веществами, в соответствии с описанием сценария развития инцидента;
программа переноса клубов и расчета их характеристик в соответствии с метеорологическими условиями (программа расчета эволюции клубов);
программа определения выпадений и концентраций в воздухе радиоактивных веществ.
В качестве входной метеорологической информации используются поля приземного ветра, поля индекса стратификации или дисперсии флуктуации направления ветра, поля осадков, построенные на весь расчетный период с определенным временным разрешением внешними программами по данным ближайших метеорологических станций. Обязательной информацией является поле ветра. Подготовка метеоинформации вынесена в отдельный программный блок с целью уменьшения времени моделирования и унификации потоков данных. Кроме того, необходимая во многих случаях прогностическая информация может быть подготовлена только в специализированных прогностических центрах.
В рамках единой технологии программного комплекса радиоэкологической информационной системы "RECASS" выполнена программная реализация подсистемы выработки вариантов контрмер.
Описываемая подсистема реализует механизмы поддержки принятия решений и выработки вариантов контрмер в случае аварийных ситуаций с целью снижения последствий радиоактивного выброса для населения, попавшего в зону его действия.
Реализованы функции отображения динамики облучения населения в интересующем пункте, расчета индивидуальных и коллективных доз с учетом принятия тех или иных контрмер (применение индивидуальных средств защиты, временное укрытие в убежищах, эвакуация по заданным маршрутам).
Расчет доз производится по методике, изложенной в [6]. В общем случае учитывается внешнее облучение от радиоактивного облака и от загрязненной поверхности земли, а также внутреннее облучение за счет ингаляции радиоактивных продуктов.
Ограничения условий применимости ПС "RECASS" определяются следующим диапазоном параметров:
|
по скорости ветра |
1-30 м/с; |
|
по высоте источника |
0 - 250 м; |
|
по расстоянию переноса |
до 50 км; |
|
по состоянию атмосферы |
от устойчивого до неустойчивого. |
Исходными данными для расчета доз являются, в общем случае, пространственно-временные поля мгновенных приземных концентраций радиоактивных продуктов в воздухе и интегральных концентраций выпадений, полученных из модельных расчетов или построенных на основе первичных данных, хранящихся в БД загрязнений.
Методика расчета рассеяния загрязняющих веществ в атмосфере при аварийных выбросах реализована также в рамках Федеральной службы по гидрометеорологии и мониторингу окружающей среды (Росгидромет) [9].
Список литературы к Приложению № 11
1. АРМ анализа и прогноза радиационной обстановки. Руководство пользователя. Книга 2. НПО "Тайфун", Обнинск, 1995.
2. Модель мезо-масштабного переноса радиоактивных веществ в атмосфере. Руководство пользователя. НПО "Тайфун", Обнинск, 2000.
3. Учет дисперсионных параметров атмосферы при выборе площадок для атомных электростанций. Руководство по безопасности (серия изданий по безопасности № 50-SG-S3). Международное Агентство по Атомной Энергии, Вена, 1982, 105 с.
4. Методы расчета распространения радиоактивных веществ в окружающей среде и доз облучения населения. М.: МХО ИНТЕРАТОМЭНЕРГО, 1992, 334 с.
5. Методы расчета распространения радиоактивных веществ с АЭС и облучения окружающего населения. № 38.220.56-84. Безопасность в атомной энергетике, т. 1, ч. 1. М: МХО Интератомэнерго, 1984.
6. Сборник правил и норм по радиационной безопасности в атомной энергетике, т. 3. МЗ СССР, М., 1989.
7. Гусев Н.Г., Беляев В.А. Радиоактивные выбросы в биосфере. Справочник. Изд. 2-е, переработанное и дополненное. М.: Энергоатомиздат, 1991, 256 с.
8. Методические указания по расчету радиационной обстановки в окружающей среде и ожидаемого облучения населения при кратковременных выбросах радиоактивных веществ в атмосферу. МПА-98. Минатом России, 1998.
9. Методика расчета рассеяния загрязняющих веществ в атмосфере при аварийных выбросах. РД 52.18.717-2009. Обнинск: ООО "Принт-Сервис", 2009, 113 с.
Приложение № 12
ПС "SULTAN"
ПС "SULTAN" предназначено для оперативного прогнозирования радиационной обстановки за пределами станции в случае аварии на АС с целью обоснования решений о проведении немедленных защитных действий в условиях минимальной информации о выбросе и метеоусловиях [1]. Организацией-разработчиком ПС "SULTAN" является ВНИИАЭС.
ПС "SULTAN" позволяет рассчитывать:
ожидаемую поглощенную дозу на щитовидную железу для персонала (на территории промплощадки и в СЗЗ) и различных возрастных групп населения за счет вдыхания радиоизотопов йода;
временную зависимость мощности дозы внешнего фотонного излучения от радиоактивных выпадений и облака на местности;
дозу внешнего облучения человека от радиоактивного облака;
дозу внешнего облучения человека от радиоактивных выпадений на местности в зависимости от времени после начала аварии;
линейные и площадные характеристики областей, нахождение человека на которых требует принятия различных экстренных мер защиты в зависимости от соответствующих уровней вмешательства.
Результаты расчета радиационных последствий аварий за пределами АС и рекомендации по экстренным защитным действиям и их объему могут базироваться на оценке ожидаемого выброса 131I в атмосферу, полученной:
в результате прямых измерений;
по данным о мощности дозы g - излучения в защитной оболочке реактора (для АС с ВВЭР-1000);
экспертным путем;
по отклику в окружающей среде.
ПС "SULTAN" позволяет проводить реконструкцию активности аварийного выброса I по экспериментальным данным о мощности дозы фотонного излучения на местности.
Важной особенностью ПС "SULTAN", отличающей его от других аналогичных программных средств, является то, что расчет аварийной дозы облучения населения может осуществляться с помощью специальных передаточных функций, связывающих дозу от всех радионуклидов с дозой только от I.
В последней версии ПС "SULTAN" имеется также возможность задавать нуклидный состав и активность выброса, когда они известны. При этом достаточно ввести данные только о выбросах ИРГ (85mKr, 87Kr, 88Кг, 133Xe и 135Xe), радиоизотопах 135I и 137Cs, которые, в основном (более чем на 95 %), определяют радиационную обстановку окружающей среды в начальный период аварии на АС.
Рекомендации о видах и масштабах экстренных защитных действий основываются на действующих критериях для принятия решений в начальный период радиационной аварии, устанавливающих верхние и нижние уровни вмешательства, а также на принципах обоснования и оптимизации с учетом конкретной обстановки и местных условий.
В ПС "SULTAN" проводится расчет как прогнозируемой (без учета вмешательства), так и предотвращаемой защитными мероприятиями дозы, по значениям которой, в соответствии с НРБ-99 и рекомендациями МАГАТЭ и МКРЗ, определяется необходимость вмешательства в нормальную жизнедеятельность населения, а также в хозяйственное и социальное функционирование территории вокруг АС в случае радиационной аварии на ядерном реакторе.
ПС "SULTAN" использует стандартную информацию о метеоусловиях, которой располагают метеостанции и службы внешней дозиметрии АС, данные о характеристике земной поверхности в направлении ветрового потока, а также минимальный набор экспертных данных о параметрах аварийного выброса.
ПС "SULTAN" разработано на базе современных представлений о механизмах рассеяния радионуклидов в атмосфере и формировании аварийной дозы облучения человека, нормативных документов, рекомендаций МКРЗ и МАГАТЭ, которые приведены в Приложении № 17.
Используемые в ПС "SULTAN" алгоритмы расчета поля приземной объемной активности нуклидов основаны на двух нормативных Гауссовых методиках для моделирования распространения примеси в атмосфере, действующих на территории России.
В первой методике для поперечной sу и вертикальной sz дисперсии при кратковременных выбросах используются формулы Смита-Хоскера [2, 3-5], а во второй методике - оригинальная аппроксимация наиболее часто используемых формул Смита-Хоскера (для sz) и Бриггса (для sу), согласно которой поперечную sу и вертикальную sz дисперсии при кратковременных выбросах рассчитывают по общей формуле, предложенной Эйри [6].
ПС "SULTAN" позволяет провести расчет аварийной дозы облучения человека при следующих ограничениях:
максимальное расстояние от источника выброса - 30 км;
скорость ветра на высоте флюгера (hф = 10 м) - 1 - 20 м/с;
состояние атмосферы - от устойчивого до неустойчивого;
минимальная эффективная высота выброса - 4 м;
максимальная эффективная высота выброса - 250 м;
минимальная продолжительность выброса - 3 мин;
максимальная продолжительность выброса - интервал времени, в течение которого погодные условия (направление и скорость ветра, состояние устойчивости атмосферы) и параметры источника выброса (эффективная высота, нуклидный состав и мощность выброса) не меняются;
эффективный максимальный диаметр аэрозолей в выбросе не превышает 10 мкм, т.е. их гравитационным осаждением из атмосферы на подстилающую поверхность можно пренебречь;
плотность выбрасываемых газов совпадает с плотностью атмосферного воздуха, т.е. диффузия тяжелых газов не рассматривается.
Вне указанных ограничений ПС "SULTAN" можно использовать только для грубых оценок.
Входными параметрами для расчетов являются: параметры источника выброса радионуклидов с учетом их физико-химических форм существования (газообразные, аэрозоли, молекулярный и органический йод); параметры, характеризующие метеорологическую обстановку; параметры, характеризующие подстилающую поверхность.
Список литературы к Приложению № 12
1. Программное средство "SULTAN" оперативного прогнозирования радиационной обстановки за пределами станции в случае аварии на АЭС. Инструкция пользователя. Утв. Техническим директором концерна "Росэнергоатом" 12.10.2000, М., 2000.
2. Методы расчета распространения радиоактивных веществ в окружающей среде и доз облучения населения. М.: МХО ИНТЕРАТОМЭНЕРГО, 1992, 334 с.
3. Методы расчета распространения радиоактивных веществ с АЭС и облучения окружающего населения. № 38.220.56-84. Безопасность в атомной энергетике, т. 1, ч. 1. М: МХО Интератомэнерго, 1984.
4. Сборник правил и норм по радиационной безопасности в атомной энергетике, т. 3. МЗ СССР, М., 1989.
5. Гусев Н.Г., Беляев В.А. Радиоактивные выбросы в биосфере. Справочник. Изд. 2-е, переработанное и дополненное. М.: Энергоатомиздат 1991, 256 с.
6. Методические указания по расчету радиационной обстановки в окружающей среде и ожидаемого облучения населения при кратковременных выбросах радиоактивных веществ в атмосферу. МПА-98. Минатом России, М., 1998.
Приложение № 13
ПС "НОСТРАДАМУС"
Одно из немногих аттестованных ПС "НОСТРАДАМУС" предназначено для оперативного (автономного) прогнозирования радиационной обстановки при выбросах радиоактивных материалов во время аварий на АС и других ядерных объектах. Система может быть использована для поддержки принятия решений в реальном времени на начальной (острой фазе) радиационной аварии [1, 2]. Организацией-разработчиком ПС "НОСТРАДАМУС" является ИБРАЭ РАН. Математическая модель, используемая в указанном ПС, относится к Лагранжево-стохастической модели распространения радионуклидов в атмосфере, которая рассмотрена в Приложении № 18. Эта модель требует существенно больше вычислительных ресурсов и времени для расчета, чем Гауссовы модели, но возможности современной компьютерной техники позволяют проводить расчеты в рамках этой модели в режиме реального времени.
ПС позволяет рассчитывать следующие данные:
мгновенные значения приземных концентраций для каждого радионуклида;
временные интегралы концентраций;
мощности дозы и дозы от каждого радионуклида (или суммарные от всех нуклидов) на разные органы, с учетом возрастных групп и по разным путям облучения:
внешнее облучение от радиоактивного облака,
внешнее облучение от загрязненной поверхности,
внутреннее облучение от ингаляционного поступления радионуклидов.
"НОСТРАДАМУС" содержит две дозиметрических модели для вычисления дозы внешнего облучения от загрязненного воздуха. По первой модели определяется доза от однородного облака бесконечной протяженности с заданной плотностью активности. Эта простая модель используется, когда размеры радиоактивного облака достаточно велики. Однако она становится некорректна, когда характерный масштаб изменения плотности активности сопоставим или меньше характерной длины пробега фотонов в воздухе. В этих случаях применяется другая дозиметрическая модель, позволяющая корректно рассчитывать дозу облучения от облака произвольной формы и размеров.
В этой модели мощность дозы рассчитывается как сумма мощностей от всех пробных точек, составляющих облако. Каждая точка рассматривается как точечный источник с известными активностью и нуклидным составом. Для того, чтобы избежать при расчете прогноза громоздких вычислений с суммированием по энергетическому спектру излучения каждого нуклида, зависимости мощности дозы от точечного источника, как функции от расстояния до точки измерения, для всех нуклидов рассчитаны заранее и введены в базу данных. Поэтому для вычисления мощности дозы от любой пробной точки необходимо лишь произвести интерполяцию между табличными значениями.
Метеорологические условия и параметры источника могут меняться со временем.
Возможное использование программы: подготовка прогнозной информации при аварийном реагировании; тренинг, обучение, подготовка и проведение деловых игр; расчеты последствий при различных сценариях развития аварийных ситуаций для обоснования безопасности объектов использования атомной энергии.
Тип объекта использования атомной энергии - любые объекты, на которых возможны аварийные выбросы радиоактивных веществ в атмосферу.
Моделируемые режимы - любые режимы, связанные с аварийными выбросами активности в атмосферу.
Расчет атмосферного переноса в простых метеорологических условиях. Программа не может использоваться для моделирования переноса в особых метеорологических условиях - в атмосферных фронтах, при бризовой циркуляции, при горно-долинной циркуляции.
Допустимые значения параметров:
|
скорость ветра |
0,5-15 м/с |
|
высота источника |
0-150 м |
|
размер области моделирования |
50 м-60 км от источника |
выброс - мгновенный, кратковременный или продолжительный (до нескольких суток).
Точность расчета определяется точностью используемых входных данных, таких, как интенсивность источника, данные о ветре, классе устойчивости атмосферы.
При наличии достоверной информации об источнике и о параметрах атмосферной дисперсии модель дает несмещенную оценку, т.е. отклонения в обе стороны практически равновероятны, и распределение имеет максимум, приходящийся на измеренное значение.
Отклонение величины приземной концентрации на расстояниях до 60 км с вероятностью 90 % укладывается в один порядок величины. Отклонение максимума концентрации на оси следа на заданном расстоянии с вероятностью 90 % не превышает 3. Не наблюдается зависимости точности прогноза от расстояния (при криволинейной форме следа вместо расстояния от источника следует использовать путь, пройденный вдоль следа). Оценка точности остается в силе и в том случае, когда приземная концентрация в заданной точке формируется при наложении нескольких траекторий.
Результаты расчета имеют некоторый случайный разброс вокруг среднего значения в силу стохастического характера модели, в которой распространение выброса представляется движением большого количества пробных точек (метод Монте-Карло). При числе пробных точек N = 2000 дисперсия результатов расчета составляет 30 %. Эта величина может быть уменьшена путем увеличения количества точек, причем уменьшение будет пропорционально 1/ÖN, но при этом увеличится время расчета.
Для расчета концентрации радиоактивной примеси в атмосфере используется полуэмпирическое нестационарное уравнение адвекции-диффузии с учетом неоднородных полей ветра и коэффициента диффузии. Метод решения - метод статистических испытаний (модифицированный метод Монте-Карло).
Исходные данные для расчета:
1) Метеорологические данные:
скорость и направление ветра на высоте 10 м (эта величина соответствует стандартному объему данных на приземном уровне, передаваемых метеостанциями и метеопостами Российской гидрометеослужбы (высотный профиль скорости ветра восстанавливается с помощью включенной в код модели пограничного слоя атмосферы);
класс устойчивости атмосферы (если нет информации по классу устойчивости, вводятся синоптические данные для его оценки: время года, суток; облачность, видимость; наличие снежного покрова);
интенсивность осадков.
2) Источник:
высота выброса;
длительность выброса;
полная активность в выбросе;
нуклидный состав выброса;
скорость гравитационного осаждения аэрозольных частиц;
скорость сухого осаждения;
коэффициент вымывания осадками.
3) Данные о местности:
Шероховатость;
рельеф (если нет данных, рельеф считается плоским).
Система может быть использована для моделирования распространения выброса любого материала, в том числе токсичных веществ в газовой и/или аэрозольной форме с последующим выпадением на почву, но имеет углубленную ориентацию на объекты атомной энергетики и выбросы радиоактивных веществ в атмосферу. Она содержит базу данных по свойствам радионуклидов (коэффициенты дозового преобразования, периоды полураспада).
Выходными данными системы являются приземные объемные активности нуклидов, плотности радиоактивных выпадений, а также прогнозируемые дозы и мощности дозы от разных нуклидов и по разным путям облучения.
Результаты моделирования в процессе расчетов отображаются на карты местности в виде контурных линий уровня или закрашенных областей. По окончании расчета варианта можно просмотреть графические временные зависимости выбранных функций в ряде точек или их зависимости от расстояния и угла. Также предусмотрены различные типы выходных текстовых файлов - документов для самостоятельной обработки с помощью других стандартных программных продуктов.
Система позволяет анализировать различные по масштабам аварии - от локальной (длительностью несколько часов) до достаточно серьезной (несколько суток по времени выброса или распространения и с зоной охвата от 50 м до 60 км). Описание модели, программного средства, части верификационных экспериментов опубликовано в [2-7].
Из сравнения с экспериментальными данными показано [2], что результаты более сложных моделей, внедренных в систему, по крайней мере, не хуже используемых нормативных методик [8-10] в их областях применимости, а при расширении этих областей адекватно описывают влияние более сложных исходных данных, заложенных в моделях.
Список литературы к Приложению № 13
1. НОСТРАДАМУС. Компьютерная система прогнозирования и анализа радиационной обстановки на ранней стадии аварии на АЭС. Инструкция пользователя. ИБРАЭ РАН, инв. № 3429, М., 2001.
2. Верификация компьютерной системы "НОСТРАДАМУС" для прогнозирования радиационной обстановки на ранней стадии аварии на АЭС. Верификационный отчет. ИБРАЭ РАН, инв. № 3431, М., 2001.
3. Arutunjan R.V., Bolshov L.D., Belikova G.V., Sorokovikova O.S. et al. Models of Radionuklides Transport i№ Atmosphere from Integrated Software Package NOSTRADAMUS. Preprint NSI-31-94, 1994.
4. Арутюнян Р.В., Беликов В.В., Беликова Г.В., Сороковикова О.С. и др. Компьютерная система НОСТРАДАМУС для поддержки принятия решений при аварийных выбросах на радиационно опасных объектах. Известия академии наук, серия Энергетика, № 4, 1995.
5. Арутюнян Р.В., Беликов В.В., Беликова Г.В., Сороковикова О.С. и др. Новые эффективные численные методики моделирования процесса распространения радионуклидов в атмосфере и их практическое использование. Известия академии наук, серия Энергетика, № 4, 1995.
6. Беликов В.В., Беликова Г.В., Фокин А.Л., Сороковикова О.С. и др. Анализ сравнения нормативных моделей переноса радионуклидов в атмосфере с лагранжевой моделью, используемой в интегрированном пакете "NOSTRADAMUS". Препринт ИБРАЭ РАН, 1996.
7. Grisenko A.I., Belov N.S., Semenov V.N., Sorokovikova O.S. The Unique Experiments on the Assessment of Accident Consequences at the Gas Transport Systems. Society for Risk Analysis-EUROPE, Stockholm, 1997, p. 724-729.
8. Сборник правил и норм по радиационной безопасности в атомной энергетике, т. 3. МЗ СССР, М., 1989.
9. Steven R. Hanna, Gary A. Briggs, Rayford P. Hosker Handbook on atmospheric diffusion. Technical Information Center U.S. Department of Energy, 1982, p. 91.
10. User's Guide for CAP88-PC. U.S. Environmental Protection Agency. Las Vegas, 1992.
Приложение № 14
ПС "ДОЗА"
ПС "ДОЗА" применяется для расчета доз облучения населения при авариях на атомных станциях с выбросом радиоактивных веществ в атмосферу. Организацией-разработчиком ПС "ДОЗА" является РНЦ "Курчатовский институт" [1, 2].
ПС "ДОЗА" рассчитывает дозы внешнего облучения от радионуклидов, находящихся в облаке и на поверхности земли, и внутреннего облучения от радионуклидов, поступивших в организм с вдыхаемым воздухом (ингаляция), и при потреблении продуктов питания.
Ограничения на применение ПС "ДОЗА"
ПС "ДОЗА" применяется на этапе проектирования АС в целях обоснования радиационной безопасности при авариях.
ПС "ДОЗА" рассчитывает эффективную дозу и эквивалентную дозу на различные органы человека в точках сектора, характеризуемых удалением от источника выброса, для следующих видов облучения:
внешнее облучение от радионуклидов, находящихся в облаке и на поверхности земли;
внутреннее облучение от радионуклидов, поступивших в организм с вдыхаемым воздухом (ингаляция) и при потреблении продуктов питания.
Допустимые значения параметров
Минимальное расстояние от источника выброса при расчете внешнего облучения от облака: точка максимума приземной концентрации; максимальное расстояние от источника: 40 км; скорость ветра на высоте флюгера (10 м): 1-30 м/с; минимальная эффективная высота источника выброса: 4 м; максимальная эффективная высота источника выброса: 250 м; минимальная продолжительность выброса: 10 мин; максимальная продолжительность выброса: интервал времени, в течение которого погодные условия не меняются.
Точность расчета, обеспечиваемая в области допустимых значений параметров
Точность расчета доз облучения населения определяется точностью используемой модели рассеивания примеси в атмосфере, погрешностью численного метода расчета параметров и выбором исходных данных.
Используемые в ПС "ДОЗА" методы расчета распространения радионуклидов в окружающей среде, основанные на Гауссовой модели рассеяния, при обосновании безопасности АС на этапе проектирования дают достаточную точность на расстояниях до десятков километров [3].
Метод численного интегрирования, примененный в ПС "ДОЗА", обеспечивает погрешность не более 0,1 %.
ПС "ДОЗА" позволяет провести консервативную оценку доз при соответствующем выборе исходных данных.
Сведения о методиках расчета, реализованных в ПС "ДОЗА"
При реализации ПС "ДОЗА" применена методика, позволяющая проводить:
расчет распространения радионуклидов в окружающей среде, основанный на модели статистической гауссовой теории атмосферной диффузии и классификации категорий устойчивости атмосферы при допущении, что подстилающая поверхность земли плоская с различными типами шероховатости;
расчет доз внешнего облучения от облака и поверхности земли и доз внутреннего облучения при ингаляции и при потреблении продуктов питания, основанный на использовании коэффициентов перехода по пищевым цепочкам [4] и базы данных по дозовым коэффициентам.
Входными параметрами для расчетов являются: параметры источника выброса радионуклидов с учетом их физико-химических форм существования (газообразные, аэрозоли, молекулярный и органический йод); параметры, характеризующие метеорологическую обстановку; параметры, характеризующие подстилающую поверхность; данные о рационе питания.
Список литературы к Приложению № 14
1. Программа ДОЗА-RRC. ОФАП-ЯР, № 393 от 28.12.96.
2. Аттестационный паспорт № 117 к программному средству "ДОЗА". Регистрационный номер паспорта аттестации ПС в Госатомнадзоре России № 117 от 02.03.2000.
3. Учет дисперсионных параметров атмосферы при выборе площадок для атомных электростанций. Руководство по безопасности (серия изданий по безопасности N 50-SG-S3). Международное Агентство по Атомной Энергии, Вена, 1982, 105 с.
4. Методы расчета распространения радиоактивных веществ с АЭС и облучения окружающего населения. № 38.220.56-84. Безопасность в атомной энергетике, т. 1, ч. 1. М: ИМХО Интератомэнерго, 1984.
Приложение № 15
ПС "GENGAUS"
ПС "GENGAUS" предназначено для оперативного прогнозирования радиационной обстановки за пределами станции в случае аварии на АС и для оценки безопасности населения при аварийных ситуациях на радиационно-опасных объектах. Владельцем ПС "GENGAUS" является Государственный научный центр Институт биофизики (ГНЦ-ИБФ). При разработке ПС "GENGAUS" использовались подходы к оценке аварий на АС, которые применялись при проведении учений в Аварийном медицинском радиационно-дозиметрическом центре ГНЦ-ИБФ.
ПС "GENGAUS" позволяет рассчитывать распространение выбросов в атмосфере по Гауссовой модели [1]. Входные параметры Гауссовой модели задаются согласно [2].
Расчет доз на население проводится по модели GENII [3], которая разработана в США и широко используется. С помощью GENII можно проводить расчеты для непрерывных и кратковременных (аварийных) атмосферных выбросов, а также для сбросов в реки и озера, при загрязнении поверхности почвы. Модель учитывает все основные пищевые цепочки поступления нуклидов в организм, процессы метаболизма и, что особенно важно, время года аварийного выброса. Компьютерные коды GENII разработаны в соответствии с национальными стандартами США и прошли несколько независимых проверок.
ПС "GENGAUS" разработан в соответствии с требованиями НРБ-99 по облучению населения в аварийных ситуациях. Дозы рассчитываются для разных моментов времени после аварии. Рассчитываются эквивалентные дозы на легкие, щитовидную железу, гонады, кожу, доза внешнего облучения и эффективная доза. Эффективная доза может рассчитываться для всех возрастных групп согласно НРБ-99. Доза на щитовидную железу рассчитывается для всех возрастных групп, согласно [2].
Список литературы к Приложению № 15
1. Гусев Н.Г., Беляев В.А. Радиоактивные выбросы в биосфере. Справочник. Изд. 2-е, переработанное и дополненное. М.: Энергоатомиздат, 1991, 256 с.
2. Методические рекомендации по выбору исходных данных и параметров при расчете радиационных последствий аварий на АЭС. ВНИИАЭС, ГНЦ-ИБФ, НПО "Тайфун", ИБРАЭ РАН. М., 2001.
3. Napier B.A., Peloquin R.A., Strenge D.L., Ramsdell J.V. GENII-The Hanford Environmental Radiation Dosimetry Software System. Volume 1: Conceptual Representation. Pacific northwest Laboratory. Washington, 1988.
Приложение № 16
Физические основы переноса примеси в атмосфере
Перенос загрязняющих субстанций в атмосфере осуществляется ветровыми потоками воздуха с учетом их мелкомасштабных флуктуаций. Осредненный поток имеет адвективную и конвективную составляющие, а их осредненные флуктуационые движения можно интерпретировать как диффузию на фоне связанного с ним основного осредненного движения.
Сформулируем задачу переноса аэрозольных субстанций (радиоактивной примеси) в атмосфере в более общем виде.
Пусть
j(x, y, z, t) - интенсивность аэрозольной
субстанции, мигрирующей вместе с потоком воздуха в атмосфере, a ![]() - вектор скорости частиц воздуха как функция
координат х, у, z и времени t, где
- вектор скорости частиц воздуха как функция
координат х, у, z и времени t, где ![]() - единичные векторы в направлении осей X,
Y, Z соответственно; Тогда перенос субстанции вдоль траектории
частиц воздуха с сохранением ее интенсивности определяется равенством нулю ее
полной производной [1].
- единичные векторы в направлении осей X,
Y, Z соответственно; Тогда перенос субстанции вдоль траектории
частиц воздуха с сохранением ее интенсивности определяется равенством нулю ее
полной производной [1].
![]() или при
или при ![]() ;
; ![]() ;
; ![]() ;
;
![]() , (1)
, (1)
но для нижней части атмосферы достаточно хорошо выполняется закон сохранения массы, определяемый уравнением неразрывности:
![]() ,
, ![]() , (2)
, (2)
что приводит к уравнению:
![]() . (3)
. (3)
Уравнение (3) можно обобщить, если учесть, что часть примеси может вступать в реакцию с внешней средой или распадаться с постоянной времени t, а также учесть источник рассматриваемой загрязняющей примеси, описываемый функцией f(x, y, z, t):
![]() , (4)
, (4)
где s =1/t.
Смысл
величины s
становится очевидным, если в (4) положить f = 0, ![]() , тогда
решение определяется как
, тогда
решение определяется как ![]() , если
, если ![]() , а величина
t
- время, за которое концентрация примеси уменьшается в e раз. Уравнение
(4) дополняется начальным условием:
, а величина
t
- время, за которое концентрация примеси уменьшается в e раз. Уравнение
(4) дополняется начальным условием:
![]() (5)
(5)
и граничным условием:
![]() ,
, ![]() , (6)
, (6)
где S
- поверхность, ограничивающая область определения искомой функции, Un - проекция
вектора ![]() на внешнюю нормаль к поверхности. Условие (6)
задает решение на той части, где воздушные массы вместе с исследуемой примесью
"втекают" в область определения функции.
на внешнюю нормаль к поверхности. Условие (6)
задает решение на той части, где воздушные массы вместе с исследуемой примесью
"втекают" в область определения функции.
Точное решение задачи (4) возможно в том случае, когда известны значения функции u, v, w в пространстве и во все моменты времени. Если же информации о компонентах вектора скорости недостаточно, то в этом случае целесообразно пользоваться различными приближениями.

Рис. 1. Спектр скорости ветра в приземном слое атмосферы [2].
Известно, что атмосфера является средой турбулентной, т.е. средой, в которой спонтанно образуются мелкомасштабные флуктуации (вихри), они диссипируются и создаются условия для новых образований. Спектр таких флуктуаций достаточно подробно изучался Ван дер Ховеном [2]. Результаты сводятся к следующему. Флуктуации сосредоточены, в основном, в двух четко разделяемых областях: в области крупномасштабных пульсаций (синоптическая область) с центром вблизи f1=0,001 цикл/час и в области мелкомасштабных пульсаций с центром около f2=80 цикл/час.
Низкочастотная область соответствует изменениям скорости ветра, вызванным прохождением циклонов и антициклонов, высокочастотная - рассматривается как турбулентные пульсации ветра, которые можно сгладить при осреднении рис. 1 [2]. В [2] получено, что величина периода осреднения T, при которой осредненные величины не зависят от T, составляет »67 мин. Физика флуктуационных эффектов изучена к настоящему времени достаточно хорошо, но математическое описание до сих пор в большинстве случаев основывается на полуэмпирических соотношениях.
Пусть
функция a
представлена в виде суммы осредненного ![]() и флуктуационного
и флуктуационного ![]() компонентов:
компонентов: ![]() и, кроме того,
и, кроме того,
![]() . (*)
. (*)
Полагаем, что a осредняется по достаточно большому интервалу времени Т:
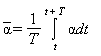 (**)
(**)
и
 . (***)
. (***)
Если
процесс переноса примеси удовлетворяет условиям (*)-(***), а концентрация
примеси и скорость ветра представлены в виде: ![]() ,
, ![]() , то
интегрируя (4) в пределах t£t£ t+T и,
используя (*)-(***) вместо (4), получим:
, то
интегрируя (4) в пределах t£t£ t+T и,
используя (*)-(***) вместо (4), получим:
![]() , (7)
, (7)
Если
Т - интервал времени, на котором функция ![]() изменяется мало, то
изменяется мало, то ![]() можно приближенно заменить на производную
можно приближенно заменить на производную ![]() и получить в результате уравнения для
осредненной составляющей:
и получить в результате уравнения для
осредненной составляющей:
![]() , (8)
, (8)
которое
отличается от (4) членом ![]() ,
ответственным за размывание потока воздушных масс, увлекающего частицы
загрязняющей примеси. Установлено, что для атмосферных процессов возможно следующее
полуэмпирическое представление компонентов вектора
,
ответственным за размывание потока воздушных масс, увлекающего частицы
загрязняющей примеси. Установлено, что для атмосферных процессов возможно следующее
полуэмпирическое представление компонентов вектора ![]() через осредненные поля субстанций:
через осредненные поля субстанций:
![]() ,
, ![]() ,
, ![]() , (9)
, (9)
где m ³
0, k ³ 0 - горизонтальный и вертикальный коэффициенты
диффузии. Учитывая представление вектора ![]() (9), вместо (8) получаем диффузионное приближение
уравнения распространения примеси в атмосфере:
(9), вместо (8) получаем диффузионное приближение
уравнения распространения примеси в атмосфере:
![]() , (10)
, (10)
где
![]() , (11)
, (11)
![]() . (12)
. (12)
В литературе, например, в [3] используется более простой вид уравнения турбулентной диффузии при m=0. Это приближение основано на том, что в природе хорошо выполняются неравенства:
![]() и
и ![]() .
.
Таким образом, при m=0 уравнение турбулентной диффузии принимает окончательный вид:
![]() (13)
(13)
с начальными условиями:
![]() (14)
(14)
и граничными условиями [4]:
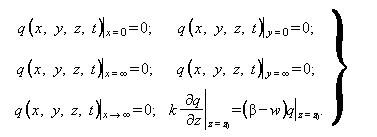 , (15)
, (15)
где b - скорость сухого осаждения; w - гравитационная скорость примеси; z0 - параметр шероховатости подстилающей поверхности.
Функциональные зависимости величин продольной - u(z), поперечной - v(z) скоростей ветра, а также коэффициента турбулентной диффузии - k(z) от высоты z от подстилающей поверхности имеют различный вид в рамках различных метеорологических моделей.
Список литературы к Приложению № 16
1. Марчук Г.И. Математическое моделирование в проблеме окружающей среды М.: Наука, 1982, 320 с.
2. Ван дер Ховен (van der Hoven J.) Power spectrum ol horizontal wind speed in the frequency range from 0,00007 to 900 cycle per hour. J. Meteorology, vol. 14, № 2, 1957.
3. Лайхтман Д.Л. Физика пограничного слоя атмосферы. Л.: Гидромет. изд-во, 1970, 340 с.
4. Бызова Н.Л., Кротова М.А., Натанзон Г.А. О граничном условии в задачах рассеяния примеси в атмосфере. Метеорология и гидрология, 1980, № 2, с. 14-20.
Приложение № 17
Анализ математических моделей переноса примеси в атмосфере
Известно, что степень влияния радиоактивных примесей при выбросах с АС определяется уровнем их приземных концентраций. Оценка последних может быть получена в рамках моделей, различающихся как способом описания диффузионных процессов, так и описанием турбулентности в пограничном слое атмосферы. Эти различия могут играть значительную роль в формировании концентрации радиоактивной примеси как на различных расстояниях от источника, так и в различных метеорологических условиях, определяя, таким образом, характерную область применимости той или иной модели. Ниже приведем краткую характеристику моделей, используемых в системе радиационного мониторинга для прогностических оценок радиоактивного загрязнения окружающей среды в условиях радиационных аварий на ОИАЭ.
В модели МАГАТЭ распределение концентраций загрязняющих частиц в атмосфере при постоянной скорости ветра описывается из предположения двойного распределения в уравнении Гаусса. Концентрация примеси, согласно этой модели, существенно зависит от двух параметров - горизонтальной sу и вертикальной sz дисперсий координат частиц примеси. При кратковременном точечном выбросе концентрация примеси описывается выражением:
 , (1)
, (1)
где РВ - мощность выброса, Бк/с; h - эффективная высота источника выбросов, [м]; иh - скорость ветра на высоте выброса, [м/с]; fR; fF; fW - безразмерные поправки на радиоактивный распад, осаждение и вымывание радиоактивной примеси соответственно. Скорость ветра на высоте источника h для однообразного равнинного рельефа местности описывается выражением:
 , (2)
, (2)
где и0 - скорость ветра на высоте флюгера; h0 - высота флюгера; m - параметр, зависящий от состояния (класса) устойчивости атмосферы. для выражений sу и sz, в настоящее время, используют формулы Смита-Хоскера [1], в соответствии с которыми эти величины принимают следующий вид:
![]() ; (3)
; (3)
![]() , (4)
, (4)
 ,
,
 ,
,
где x - расстояние от источника выбросов, c1, c2, c3, a1, a2, b1, b2, d1, d2 - параметры, зависящие от класса устойчивости атмосферы [1, 2].
К основным недостаткам Гауссовых моделей можно отнести слабую обоснованность использования закона Гаусса для описания распределения примеси по вертикали, а также условность типизации (условное разделение состояния устойчивости атмосферы на шесть классов) метеорологических условий [3], хотя нельзя отрицать и определенные удобства при таком подходе. Разнообразие Гауссовых моделей в значительной степени связано с различными методами оценок этих величин. Наиболее широко используемыми методами являются: метод Пасквилла-Гиффорда, основанный на номограммах для шести классов устойчивости атмосферы; метод, основанный на учете вертикального градиента температуры; метод, основанный на учете флуктуации ветра; метод "разделенной сигмы" и т.д. Модель отличается значительной простотой в использовании, ее рекомендуют применять для расстояний (в направлении ветра) не более 10 км при высоте источников не выше 100 м.
В основе Эйлеровой и Лагранжевой моделей лежит возможность математического представления движения жидкости (воздушной среды) в переменных Эйлера или Лагранжа. В первом случае аргументом является совокупность координат точек пространства, а компоненты вектора скорости жидкости в данной точке пространства являются функциями этих координат и времени. Во второй рассматривают некоторую бесконечно малую частицу жидкости в фиксированный момент времени t0 с координатами (x0, y0, z0) и, перемещаясь вслед за ней, рассматривают ее координаты в последующие моменты как функции времени и ее начальных координат. Таким образом, во втором случае скорости частиц представляют собой производные от координат по времени. Используя каждый из подходов в той или иной модели получают модели Эйлера или Лагранжа. Модель Эйлера обладает рядом преимуществ по сравнению с Гауссовыми моделями, поскольку позволяет учесть нестационарность источника выброса, влияние пространственных и временных вариаций метеорологических величин на распространение примеси, использовать полуэмпирические модели приземного слоя атмосферы для более реалистического описания турбулентности. Эйлеровы модели также различаются между собой в зависимости от способа получения метеорологических величин - скорости ветра и коэффициента турбулентной диффузии. К такого типа моделям относится и модель работы [4], в которой метеорологические параметры получают на основе решений замкнутой системы уравнений пограничного слоя атмосферы. Эти модели в отличие от Гауссовых достаточно сложны, требуют значительного времени счета на ЭВМ, что до недавнего времени сдерживало их практическое использование. Однако широкое распространение персональных ЭВМ высокого уровня полностью решило эти проблемы, что и позволяет использовать эти модели в режиме реального времени (on-line) для проведения диагностических прогнозов по загрязнению внешней среды при авариях на АС.
При заданных метеорологических параметрах (продольной и поперечной скоростях ветра, коэффициенте турбулентной диффузии и поперечной (относительно направления распространения примеси) дисперсии) не существует принципиальных проблем расчета концентраций в любой точке пространства в направлении выброса примеси. Если и возникают определенные затруднения в оценке концентрации в поле пространственно-временных измерений скорости ветра, то они, в первую очередь, связаны с некорректным измерением этих метеовеличин. При сложной орографии поверхности обычно используют дополнительные данные [5], а при оценке концентрации на расстояниях свыше 50-100 км необходимо использовать данные метеорологической сети Роскомгидромета, но эти проблемы уже не относятся к компетенции АС.
Определенное преимущество перед Эйлеровыми имеют модели, основанные на Лагранжевом подходе. В этих моделях непрерывная струя обычно представляется в виде последовательности дискретных клубов. Для каждого клуба рассчитывается траектория его движения в меняющемся во времени и пространстве поле ветра и рассчитывается диффузионный перенос в направлениях перпендикулярных к траектории. Концентрацию примеси в любой точке пространства представляют как сумму вкладов от каждого лагранжевого элемента.
В Лагранжево-Эйлеровой модели переноса и рассеяния примеси [6] ее горизонтальный перенос описывается с помощью понятия Лагранжевой траектории движения клуба примеси, а для описания атмосферной диффузии клуба в вертикальном направлении на каждом шаге вычисления горизонтальной траектории решают полуэмпирическое одномерное уравнение турбулентной диффузии. В горизонтальном направлении, перпендикулярном траектории клуба, концентрация примеси описывается Гауссовой функцией с дисперсией, зависящей от продолжительности распространения клуба и устойчивости атмосферы. Модель достаточно сложна и при ее использовании в целях прогнозирования загрязнения окружающей среды кроме измерений скорости ветра, температуры, направления ветра на нескольких уровнях в приземном слое атмосферы, необходимых для расчета таких параметров как масштаб Монина-Обухова L и динамической скорости V*, требуются измерения вектора скорости ветра на эффективной высоте и величины геострофического ветра на высоте пограничного слоя атмосферы, что, в свою очередь, требует шаропилотного зондирования атмосферы. Лагранжево-Эйлерову модель наиболее целесообразно использовать для оценки загрязнения воздушного бассейна при трансграничном переносе радиоактивной примеси (свыше 1000 км и более).
Таким образом, из краткого анализа моделей следует, что каждая из рассмотренных имеет как преимущества, так и недостатки, поэтому результаты сравнения расчетных и экспериментальных данных должны показать преимущество той или иной модели, используемой для оценки и прогнозирования радиоактивного загрязнения окружающей среды при выбросах АС в регионе, определяемом размерами зоны наблюдения (R ~ 30¸40 км).
Учитывая такие особенности моделей, естественно, что выбор (в зависимости от рода задач, для которых модель используется) следует остановить на тех, применение которых наряду с необходимыми метеорологическими приборами обходится дешевле.
Список литературы к Приложению № 17
1. Гусев Н.Г., Беляев В.А. Радиоактивные выбросы в биосфере. Справочник. М.: Энергоатомиздат 1991, 256 с.
2. Методы расчета распространения радиоактивных веществ в окружающей среде и доз облучения населения. М.: МХО ИНТЕРАТОМЭНЕРГО, 1992, 334 с.
3. Глущенко А.И., Лайхтман Д.Л., Натанзон Г.А., Петров О.Г., Хамьянов Л.П. О выборе метода расчета рассеяния радиоактивных примесей, выбрасываемых АЭС в атмосферу. Атомные электрические станции, вып. 4, 1981, с. 154-158, М.: Энергоиздат, Сб. статей под общ. ред. Л.П. Воронина, 239 с.
4. Елохин А.П., Pay Д.Ф. Гибридный метод прогнозирования загрязнения окружающей среды радиоактивной примесью, поступающей в атмосферу при выбросах с АЭС. В сб. Методы расчета распространения радиоактивных веществ в окружающей среде и доз облучения населения. М.: МХО МНТЕРАТОМЭНЕРГО #, 1992 с. 91, 283-303.
5. Учет дисперсионных параметров атмосферы при выборе площадок для атомных электростанций. Руководство по безопасности (серия изданий по безопасности № 50-SG-S3). Международное Агентство по Атомной Энергии, Вена, 1982, 105 с.
6. Гаргер Е.К., Буйков М.В., Талерко Н.Н. Сравнение различных методик распространения примеси с экспериментальными данными. Международный семинар по вопросу разработки методик расчета размеров зон планирования и подготовки мероприятий по защите населения в случае запроектной аварии на АЭС и совещание по обсуждению содержания методики оценки изотопного состава, величины активности и характера аварийного выброса в атмосферу в зависимости от времени, активности в топливе и состоянии барьеров и систем безопасности. Сборник докладов. Варна, НРБ, 7-12 мая 1990 г.
Приложение № 18
Дифференциальная модель распространения радионуклидов в атмосфере
Представляемая модель описывает распространение примесей в атмосфере. Предполагается, что примеси могут быть в газовой и/или аэрозольной форме. При этом газовые компоненты (если они есть) могут иметь плотность, приблизительно равную плотности воздуха, и эффекты плавучести не учитываются.
Модель основана на том, что распространение примеси в атмосфере описывается полуэмпирическим уравнением адвекции-диффузии. Это уравнение переноса и диффузии имеет вид:
 , (1)
, (1)
где с - объемная концентрация радиоактивной примеси в воздухе;
![]() ;
; ![]() - горизонтальные компоненты скорости ветра;
- горизонтальные компоненты скорости ветра;
![]() ;
; ![]() - вертикальная компонента скорости ветра;
- вертикальная компонента скорости ветра;
Wg - скорость гравитационного оседания (отлична от 0 (Wg>0) для аэрозольной составляющей);
Kx(x, y, z, t), Ky(x, y, z, t) - коэффициенты горизонтальной диффузии;
Kz(x, y, z, t) - коэффициент вертикальной диффузии;
Q(x, y, z, t) - мощность источника выброса;
S - член, учитывающий вымывание осадками, радиоактивный распад и появление радионуклида в результате реализации цепочек превращений других радионуклидов, содержащихся в источнике выброса.
Граничные условия для (1) следующие.
При z=0 задается поток примеси на подстилающую поверхность за счет сухого осаждения:
![]() ,
,
где Vd - скорость сухого осаждения.
На верхней границе расчетной области z=Zm предполагается отсутствие потока
![]() .
.
На
боковых (вертикальных) границах расчетной области предполагается условие: ![]() , где
, где ![]() - направление нормали к боковой границе).
Следует отметить, что боковые границы располагаются далеко от центра струи и
характер граничных условий не влияет на решение.
- направление нормали к боковой границе).
Следует отметить, что боковые границы располагаются далеко от центра струи и
характер граничных условий не влияет на решение.
Величина Zm выбирается таким образом, чтобы она была несколько больше высоты пограничного слоя атмосферы (ПСА): Zm=1,2-1,5Hm (определение высоты ПСА обсуждается ниже). Если высота ПСА меняется со временем в течение расчета, то Zm должно быть больше максимального значения Hm.
Скорость ветра и коэффициенты диффузии в уравнении (1) считаются заданными функциями координат и времени.
Метод решения уравнения переноса
Уравнение (1) с неоднородным полем скорости ветра при неизотропной турбулентности (без учета вымывания и цепочек превращений) решается методом статистических испытаний (метод Монте-Карло). Этот метод можно наглядно интерпретировать следующим образом. Облако примеси представляется в виде большого количества пробных частиц (точек), каждая их которых движется в соответствии со скоростью ветра и, кроме того, подвергается случайным смещениям, моделирующим турбулентное рассеивание. Объемная концентрация точек ассоциируется с концентрацией примеси. Рассмотрим сначала решение уравнения вдали от источника и без учета распада и вымывания.
Координаты точек удовлетворяют системе стохастических уравнений [1, 2]:
![]() ;
; ![]() ;
; ![]() , (2)
, (2)
где
![]() ,
, ![]() , (2a)
, (2a)
![]() .
.
Первые члены в правых частях последних трех соотношений - компоненты усредненной скорости ветра. Вертикальная скорость частицы отлична от скорости ветра, даже если гравитационная скорость равна нулю. Добавка W¢¢ необходима, как будет видно дальше, для согласования решения при неоднородном коэффициенте вертикальной диффузии. Ее величина будет найдена позднее.
U1, V1, W1 - компоненты пульсации скорости ветра вдоль траектории частиц, случайные функции. Предполагается, что значения пульсационной скорости в разные моменты времени на траектории частицы не скоррелированы между собой (характерное время затухания корреляций меньше временного шага интегрирования). Отметим, что движение пробных точек не моделирует реальных траекторий частиц примеси. Описываемая процедура представляет способ решения полуэмпирического уравнения (1).
Проинтегрируем систему стохастических уравнений (2) на интервале dt с учетом указанных предположений о корреляционной функции скоростей:
![]() ,
, ![]() ,
, ![]() ,
,
где dx, dу, dz - случайные смещения. Они удовлетворяют следующим соотношениям:
![]() ,
, ![]() ,
, ![]()
Здесь
![]() - коэффициенты, зависящие от корреляционных
функций скоростей. Значок <.> означает усреднения по статистическому
ансамблю. Теперь изменения координат точек в конкретной реализации процесса за
шаг интегрирования может быть записано в виде:
- коэффициенты, зависящие от корреляционных
функций скоростей. Значок <.> означает усреднения по статистическому
ансамблю. Теперь изменения координат точек в конкретной реализации процесса за
шаг интегрирования может быть записано в виде:
![]() ,
, ![]() ,
, ![]() , (3)
, (3)
где
ax,
aу, аz - случайные величины с Гауссовым
распределением вероятности, с нулевым математическим ожиданием и дисперсией ![]() ,
, ![]() ,
, ![]() .
.
Начальные условия для системы (2) следующие. Траектория каждой точки начинается в объеме источника примеси:
![]() ;
; ![]() ;
; ![]() ,
,
где XS, YS, ZS - координаты источника.
Скорость рождения точек в источнике пропорциональна интенсивности источника.
Уравнение (1) описывает изменения траектории Лагранжевых частиц. Траектория любой Лагранжевой частицы есть случайный Марковский процесс с независимыми приращениями.
Этот процесс можно связать с концентрацией примеси. Объемные концентрации примеси могут быть получены при помощи функции плотности вероятности m(x, y, z, t, x0, y0, z0, t0) - того, что частица, появившаяся в точке с координатами x0, y0, z0 в момент времени t0, окажется в момент времени t в точке с координатами x, y, z.
Объемная концентрация следующим образом выражается через функцию плотности вероятности
 (4)
(4)
где V - объем в атмосфере, который занимает источник.
Можно показать, что если в (3) принять:
![]() ;
; ![]() ;
; ![]() ,
,
то объемная концентрация, соответствующая (4), удовлетворяет следующему уравнению:
 (5)
(5)
или
![]()
![]() (6)
(6)
В этом уравнении Ur, Vy и Wy - компоненты регулярной скорости движения частиц как функции координат, определяемые (2a). В (6) учтено, что горизонтальные компоненты, согласно (2a), равны компонентам усредненной скорости ветра Ur=U, Vy=V.
Как
правило, производными от коэффициентов горизонтального турбулентного обмена по
сравнению с горизонтальной скоростью ветра можно пренебречь и положить ![]() . Для
вертикальной компоненты это не так. Согласно (2a):
. Для
вертикальной компоненты это не так. Согласно (2a):
![]()
Если
выбрать ![]() и подставить в (6), то последнее уравнение
примет следующий вид:
и подставить в (6), то последнее уравнение
примет следующий вид:
 ,
,
полностью идентично (1) (без учета объемных источников и стоков). Учет объемных стоков и граничных условий при реализации случайного движения точек описывается ниже.
Таким
образом, для того, чтобы концентрация примеси, выражаемая выражением (4),
удовлетворяла исходному уравнению (1), необходимо, чтобы вертикальная скорость
движения частиц отличалась от скорости ![]() на величину
на величину ![]()
![]() .
.
В
некоторых моделях подобного типа член ![]() в последнем уравнении системы (3) не
учитывался [3].
Это приводит к нереалистичному распределению примеси по высоте, скоплению
примеси у поверхности, завышенным значениям выпадения. Так как в нижних слоях атмосферы
коэффициент вертикальной диффузии быстро растет с высотой, то за счет этого
появляется эффективная средняя вертикальная скорость (на фоне турбулентных
пульсаций).
в последнем уравнении системы (3) не
учитывался [3].
Это приводит к нереалистичному распределению примеси по высоте, скоплению
примеси у поверхности, завышенным значениям выпадения. Так как в нижних слоях атмосферы
коэффициент вертикальной диффузии быстро растет с высотой, то за счет этого
появляется эффективная средняя вертикальная скорость (на фоне турбулентных
пульсаций).
Граничные условия
Для учета граничного условия, связанного с потоком на подстилающую поверхность, применяется следующий алгоритм. Рассмотрим частицы, находящиеся в объеме dx dy dz вокруг точки х, у. По определению скорость осаждения на поверхность равна c(Vd+Wg), где c - концентрация в данной точке, рассчитанная указанным выше способом. За один временной шаг из данного объема выпадет активность dA, равная
![]() . (7)
. (7)
Выпавшая активность распределяется равномерно по площади dxdу. Одновременно полная активность всех точек в объеме dxdуdz уменьшается на dA, а активность каждой частицы в этом объеме - на dA/N (N - число частиц в объеме). При этом полное количество частиц в расчете не меняется.
Скорость сухого осаждения может иметь разные значения для разных типов аэрозолей. Для мелких аэрозольных частиц, когда можно пренебречь гравитационным осаждением, наличие в выбросе аэрозолей с разными скоростями сухого осаждения учитывается следующим образом. Диапазон скоростей сухого осаждения делится на ряд групп, и выражение (7) для величины выпавшей активности заменяется на:
![]() , (7a)
, (7a)
где ai - доля аэрозолей со скоростью сухого осаждения Vdi (i - номер группы). Движение пробных частиц при этом не меняется.
Если в выбросе присутствуют аэрозоли с разными скоростями гравитационного оседания, то пробные частицы делятся на группы, каждая из которых имеет свою гравитационную скорость оседания.
Разбиение на группы по гравитационному осаждению требует знания распределения аэрозольных частиц в выбросе по размерам. Способ усреднения размеров в каждой группе (если группа имеет достаточно широкий разброс размеров) зависит от поставленной задачи (он может сохранять полную массу частиц в группе или полную поверхность).
Для крупных частиц (d > 50 мкм) осаждение на поверхность определяется в основном гравитацией. Для более мелких частиц сухое осаждение определяется турбулентным диффузионным потоком на поверхность, и скорость сухого осаждения зависит от метеорологических условий, от характера поверхности, химических свойств аэрозольных частиц и поверхности.
В отсутствие информации о распределении размеров параметры групп по гравитационному оседанию и сухому осаждению задаются пользователем. Так, в соответствии с документом [4] принимается, что аэрозольные частицы, возникающие при разрушении активной зоны реактора при тяжелой аварии, будут иметь размеры микронного диапазона. Гравитационным оседанием таких частиц можно пренебречь, скорость сухого осаждения берется порядка 0,8 см/сек для всех нуклидов, кроме изотопов йода, для которых она принимается 2 см/сек и 0,01 см/сек для молекулярной и органической форм соответственно. Значения скорости сухого осаждения для различных нуклидов и типов подстилающей поверхности приведены в Приложении № 5.
Список литературы к Приложению № 18
1. Boughton B.A., J.M. Delauentis, W.E. Dunn A Stochastic Model of Particle Diffusion in the Atmosphere. Boundary Layer Meteor, v. 40, 1987, pp. 147-163.
2. Zanetty P. New Monte Carlo scheme for simulation lagrangian particle diffusion with wind shear effects. Appl. math. modelling, V. 8, 1984, pp. 188-192.
3. Костриков А.А., Новицкий М.А. Численное моделирование распространения примеси от точечного источника в условиях бризовой циркуляции. Труды ИЭМ, вып. 37(120), 1986, с.25-38.
4. Методические рекомендации по выбору исходных данных и параметров при расчете радиационных последствий аварий на АЭС. Утверждено Ген. директором ВНИИАЭС А.А. Абагяном, директором ГНЦ-ИБФ Л.А. Ильиным, Ген. директором НПО Тайфун А.Д. Орлянским, директором ИБРАЭ РАН Л.А. Большовым, Техническим директором концерна Росэнергоатом Б.В. Антоновым. М., 2001
Приложение № 19
Нетрадиционные методы оценки радиоактивного загрязнения окружающей среды
Традиционные методы прогнозирования радиоактивного загрязнения окружающей среды типа АСКРО оправдывают себя при наличии фиксированных источников радиационной опасности. Однако аварии на ФГУП НПО "МАЯК" (1957 г.) и в Томске (1993 г.) убеждают в необходимости разработки дистанционных (бесконтактных для человека) средств оценки загрязнения окружающей среды. В качестве таких средств могут служить переносные и стационарные радиолокационные станции [1], или радиоуправляемые беспилотные дозиметрические комплексы [2-4]. Преимущество таких систем перед традиционными очевидны - это бесконтактность человека с радиоактивным загрязнением окружающей среды, высокая мобильность оборудования, под последним понимается возможность установки таких средств на обычном, специализированном автотранспорте и различных авиасредствах.
Идея использования методов радиозондирования атмосферы для обнаружения в ней ионизационных образований техногенного происхождения [1] основана на особенностях распространения электромагнитных волн в плазме, которые хорошо изучены при распространении их в ионосфере. Вопросу же распространения электромагнитных волн в плазме, возникающей в пограничном слое атмосферы в результате промышленной деятельности ряда предприятий, не уделялось достаточного внимания в силу того, что источники плазмы имеют техногенное происхождение. Суть применения метода радиозондирования областей с источниками радиоактивных выбросов и загрязненной радиоактивными аэрозолями подстилающей поверхности состоит в оценке коэффициента отражения, представляющего собой отношение квадратов амплитуд отраженной и падающей радиоволн от ионизационных образований (плазмоидов), возникающих в атмосфере при ионизации воздушной среды ионизирующим излучением радионуклидов, распространяющихся в атмосфере в результате радиационных аварий. По значению этого коэффициента отражения и ряда измеряемых метеорологических (относительной влажности воздуха, температуры окружающей среды, давления, вертикальной составляющей скорости воздушного потока) и радиационных (спектральный состав фотонного излучения) параметров можно судить о величине PВ объемного источника, если радиозондированию подвергается источник радиоактивных выбросов, или о величине плотности поверхностного загрязнения q0, если зондируется подстилающая поверхность [5-7] в общем случае зависимость коэффициента отражения от PВ объемного источника выбросов с учетом температурно-влажностного режима пограничного слоя атмосферы имеет степенной характер: R~(Pв)D, где 0,25 £ D £ 0,5; R - коэффициент отражения. Аналогичная зависимость имеет место и относительно плотности поверхностного загрязнения q0.
Идея использования радиоуправляемого беспилотного дозиметрического комплекса [2-4] не нова, поскольку аналогична известному методу авиационной разведки, который широко использовался для обнаружения залежей урановых руд. Новизна метода состоит в том, что для определения объемной активности газоаэрозольной радиоактивной примеси, распространяющейся в атмосфере в результате радиационной аварии, используется не аспирационный метод, широко применяемый для этих целей, а совокупность спектрометрического и дозиметрического оборудования, позволяющая проводить измерение в режиме реального времени. Последнее дает возможность проводить измерения объемной активности непосредственно в облаке газоаэрозольной радиоактивной примеси, распространяющейся в атмосфере в результате радиационной аварии, что обеспечивает оперативность получения информации при развитии аварии, а также позволяет производить прогностические оценки радиоактивного загрязнения окружающей среды и его последствий. Кроме того, беспилотный дозиметрический комплекс с успехом может быть использован для независимой проверки эффективности существующих систем радиационного мониторинга указанных объектов, для радиационного мониторинга ОИАЭ при их штатной работе, радиационного мониторинга акваторий, используемых для сброса, с целью изучения вопросов миграции радионуклидов, распространяющихся в водной среде, и радиационного мониторинга зон (подстилающей поверхности), ранее подверженных радиоактивному загрязнению.
Список литературы к Приложению № 19
1. Боярчук К.А., Кононов Е.Н., Ляхов Г.А. Радиолокационное обнаружение областей локальной ионизации в приземных слоях атмосферы. Письма в ЖТФ, 1993, т. 19, вып. 6, с. 67-72.
2. Елохин А.П., Рау Д.Ф., Пархома П.А. Способ дистанционного определения концентрации радионуклидов в воздушном выбросе радиационно-опасных предприятий и устройство его осуществления. Федеральный институт промышленной собственности России. Заявка МПК G01T1/167 № 2006124100/28 с приоритетом от 06.07.06. Патент № 2299451, бюл. № 14, решение о выдаче патента от 07.12.2006.
3. Елохин А.П., Сафоненко В.А., Улин С.Е., Дмитренко В.В., Пчелинцев А.В., Пархома П.А. Применение беспилотного дозиметрического комплекса для определения концентрации радионуклидов в атмосфере в условиях радиационных аварий. Ядерные измерительно-информационные технологии, № 3(23), 2007, с. 42-59.
4. Елохин А.П., Сафоненко В.А., Пчелинцев А.В., Пархома П.А. Метод дистанционного определения концентрации радионуклидов в воздушном выбросе радиационно-опасных предприятий, Экологические системы и приборы, № 5, 2007, с. 9-15.
5. Елохин А.П. Способ дистанционного контроля радиационной обстановки зон с объектами радиоактивных выбросов и загрязнений. Заявка на изобретение РФ № 99108898. Приоритет от 21.04.99, Москва, Федеральный Институт Промышленной Собственности России (ФИПСР), 18 с. Патент на изобретение № 2147137 от 27.03.2000.
6. Елохин А.П. К вопросу о продольной устойчивости ионизационных образований техногенного происхождения. ЖТФ, № 8, 2001, c. 98-108.
7. Елохин А.П. Продольная устойчивость ионизационных образований техногенного происхождения. Атомная энергия, том 89, вып. 6, 2000, с. 480-494.
Приложение № 20
Метод определения необходимого и достаточного количества датчиков АСКРО, размещаемых на промплощадке и в СЗЗ ОИАЭ
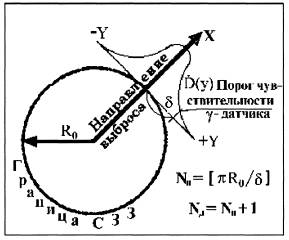
Рис. 1. Иллюстрация выбора оптимального количества датчиков АСКРО
К размещению постов контроля в СЗЗ предъявляют демографические, экономические и экологические требования. Демографические - определяются критерием численности населения: пост контроля устанавливается в населенном пункте с числом жителей не менее 5 тыс. человек [1]. Экономические требования сводятся к ограничению числа постов (датчиков), что обусловлено высокой стоимостью линий связи, оборудования (датчиков, приемопередающих информацию устройств, систем персональных ЭВМ), зарплатой обслуживающего персонала, затратами на социальные нужды и т.д. Экологические требования сводятся к обеспечению высокой степени информативности об уровнях загрязнения окружающей среды при любом направлении выброса, чего можно достигнуть увеличением числа постов контроля на промплощадке и в СЗЗ. Таким образом, число постов контроля АСКРО играет значительную роль не только как одна из наиболее важных составных частей системы, но и как часть, формирующая стоимость системы в целом.
Для определения необходимого и достаточного числа датчиков, способных зарегистрировать факел или облако радиоактивных выбросов, распространяющихся от источника при любом направлении ветра 0£j£2p и при любом состоянии устойчивости атмосферы, воспользуемся идеей работы [2], но в качестве "дозовых критериев" выберем мощность дозы внешнего облучения, а в качестве порога - мощность дозы внешнего облучения для населения [3]. Число постов контроля в этом случае найдем следующим образом. Положим, что радиоактивная примесь рассеивается с высоты hэф при наихудших метеорологических условиях, в качестве которых можно рассматривать категорию устойчивости типа F из класса устойчивости модели Пасквилла-Гиффорда [4]. Этот класс характеризуется сильным ветровым переносом и слабой поперечной диффузией факела выбросов. На подстилающей поверхности на расстоянии R ~ 3* км от источника на проекции оси выброса задают мощность дозы внешнего облучения, равную предельно допустимой для группы "В" (население), полагая, что такую мощность дозы создает факел выброса, распространяющийся в заданном направлении в выбранной точке (рис. 1).
На подстилающей поверхности рассчитывают распределение мощности дозы в направлении, перпендикулярном к радиусу, считая, что в максимуме распределения, т.е. на границе зоны по радиусу и достигается предельно допустимая мощность дозы. В полученном распределении находят расстояние, на котором мощность дозы оказывается равной порогу чувствительности датчика (Dу)min. Если это расстояние d, то необходимое число датчиков определится целой частью отношения Nн=[2pR/2d]=[pR/d], а достаточное - на единицу больше Nд=Nн+1. При классе устойчивости F равно Nн=22¸24. При ином классе устойчивости (например, А), когда скорость переноса невелика, но значительна поперечная диффузия примесей, при неизменных остальных параметрах выброса (мощность выброса, радионуклидный состав) Nн=14¸16, что нетрудно понять из рис. 2. Таким образом, наименьшее число датчиков, размещаемых в СЗЗ и регистрирующих факел выбросов при любом направлении ветра, для класса устойчивости не ниже F должно отвечать наихудшим условиям и составлять 22¸25. Следует отметить при этом, что с повышением чувствительности датчика, т.е. с уменьшением порога до 0,01m Зв/ч (последнее может быть получено за счет повышения чувствительности непосредственно регистрирующего элемента и путем вычитания радиационного фона) значение d увеличится, а Nн - уменьшится без потери чувствительности системы в целом (наглядный пример того, как повышение качества дает количественный результат).

Рис. 2. Распределение мощности дозы в направлении, перпендикулярном оси факела выбросов при Х=2750 м при устойчивом m0= 25,4 и неустойчивом m0= -15,8 состояниях атмосферы [5]
Таким образом, алгоритм определения необходимого и достаточного количества датчиков АСКРО, размещаемых на промплощадке и в СЗЗ ОИАЭ, сводится к:
1. Заданию радиуса СЗЗ R0.
2. Определению эффективной высоты выброса hэф.
3. Определению направления выброса радиоактивной примеси в атмосферу;
4. Проведению расчета пространственного распределения мощности дозы внешнего облучения на высоте 1 м в локальной системе координат для наихудшего состояния устойчивости атмосферы (состояния типа F в рамках классификации модели Пасквилла-Гиффорда).
5. Построению кривой распределения мощности дозы внешнего облучения в локальной системе координат XY на границе СЗЗ (рис. 1) (максимум распределения (на оси Y) соответствует предельному значению мощности дозы для населения).
6. Нахождению на построенной кривой распределения мощности дозы D'(X) значения, соответствующего величине предельной чувствительности датчика фотонного излучения системы АСКРО и соответствующего этой величине значения абсциссы X¢=d.
7. Определению необходимого количества числа датчиков фотонного излучения системы АСКРО целой частью отношения: Nн=[2pR0/2d]=[pR0/d].
8. Определению достаточного количества числа датчиков фотонного излучения системы АСКРО выражением Nд=[pR0/d]+1.
Полученные значения Nн и Nд будут отвечать соответственно необходимому и достаточному количеству датчиков фотонного излучения системы АСКРО, размещаемых вокруг ОИАЭ.
Указанную процедуру оценки необходимого и достаточного количества числа датчиков фотонного излучения системы АСКРО целесообразно проводить, предварительно набирая статистические данные по сезонным и годовым изменениям скорости ветра и температуры, характеризующим состояние устойчивости атмосферы, в рамках исследований метеорологических особенностей региона, в котором размещается АС.
Список литературы к Приложению № 20
1. Автоматизированная система контроля радиационной обстановки в районе расположения атомных станций (АСКРО). Общие технические требования к системе и структуре размещения в районе расположения атомной станции. М.: Минатомэнерго СССР, 1988.
2. Кюммель М. Разработка оптимальной сети измерений для проведения контроля окружающей среды на АЭС. В кн. Обеспечение радиационной безопасности при эксплуатации АЭС. Кн. 5, М.: Энергоатомиздат, 1984, с. 78-89.
3. Елохин А.П. Принципы размещения датчиков мощности дозы вокруг АЭС. Атомная энергия. Т.76, Вып. 3, 1994, с. 188-193.
4. Учет дисперсионных параметров атмосферы при выборе площадок для атомных электростанций. Руководство по безопасности (серия изданий по безопасности № 50-SG-S3). Международное Агентство по Атомной Энергии, Вена, 1982, 105 с.
5. Елохин А.П. Оптимизация методов и средств автоматизированных систем контроля радиационной обстановки окружающей среды. Диссертация на соискание ученой степени доктора технических наук. М.: МИФИ, 2001, 325 с.
______________________
* В настоящее время происходит пересмотр границ СЗЗ АС и зон наблюдения в сторону их уменьшения.
Приложение № 21
Принцип размещения детекторов фотонного излучения АСКРО на промплощадке и в СЗЗ ОИАЭ
Рассмотренный в Приложении № 20 принцип размещения постов контроля в С33 целесообразен лишь при условии, что примеси при нештатной работе или аварийной ситуации выбрасываются из вентиляционных труб АС. В этом случае наиболее важные параметры выброса, такие, как начальные температура T0 и давление струи P0, мощность выброса PВ, радионуклидный состав примесей или спектральный фотонного излучения, могут быть измерены специальными датчиками или их совокупностью, установленными в устье венттрубы. Иная ситуация возникает при несанкционированном выбросе примесей в виде перегретой газовой струи из отверстий, клапанов, неплотностей сосудов, рваных отверстий или щелей, возникающих в случае взрыва или разрыва резервуаров, находящихся под высоким давлением и высокой температурой. В этом случае экспериментально почти невозможно определить ни параметры струи, выбрасываемой из отверстий, ни объемную активность примесей, ни их радиационные характеристики, поскольку не известен спектр или средняя энергия фотонного излучения, и, в конечном счете, невозможно определить масштабы радиоактивного загрязнения окружающей среды и оценить его экологические последствия, так как подобные аварии являются крайне редкими и не могут быть прогнозируемыми. Разработка же универсальной аппаратуры, которую можно было бы использовать для определения указанных параметров и характеристик в любых ситуациях, - задача почти невыполнимая и, кроме того, может привести к резкому удорожанию АС. Тем не менее, радиоактивное загрязнение окружающей среды в случае мощного нестационарного импульсного выброса примесей через отверстия может быть успешно оценено при использовании показаний технологических датчиков, устанавливаемых в сосудах и определяющих температуру и давление среды, и показаний датчиков АСКРО, определяющих мощность дозы внешнего облучения от облака, образовавшегося в результате выброса. При этом датчики на промплощадке и в СЗЗ должны быть расположены по определенному правилу, которое требует, чтобы расстояние от возможного источника радиационной опасности (АС) до любого датчика было строго различно. Чтобы убедиться в этом, достаточно рассмотреть в общем случае выражение для мощности дозы в точках Pi,j,k=P(xi,yj,zk), расположенных на подстилающей поверхности, от объемного источника (облака) с распределением объемной активности в нем q(x, y, z):
 , (1)
, (1)
где a(E) - зависимость
чувствительности детектора от энергии фотонного излучения примесей в облаке; ma(E), m(E) - коэффициенты
передачи энергии и линейного ослабления фотонного излучения в воздухе
соответственно; ![]() - фактор накопления; a(Е), b(Е)
- известные функции энергии [1];
j(E) - подлежащий
определению дифференциальный спектр фотонного излучения примесей; x, y,
z - текущие координаты; xi, yj, zk, , - координаты датчиков АСКРО; V -
область интегрирования;
- фактор накопления; a(Е), b(Е)
- известные функции энергии [1];
j(E) - подлежащий
определению дифференциальный спектр фотонного излучения примесей; x, y,
z - текущие координаты; xi, yj, zk, , - координаты датчиков АСКРО; V -
область интегрирования; ![]() ;
; ![]() .
.
Предполагая кратковременность выброса, можно пренебречь его смещением относительно оси симметрии. Требование кратковременности существенно упрощает метод оценки мощности дозы, создаваемой облаком, тогда как оценка мощности дозы в динамическом режиме распространения требует учета не только деформации облака, но и учета метеорологических факторов атмосферы, особенностей подстилающей поверхности и т.д. (ниже будет показано, как обойти и эти трудности).
Координаты центра масс облака определим следующим образом:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Полагая,
что расстояние ![]() от точки центра масс до любого поста контроля
АСКРО значительно больше характерного размера облака, объемную активность q(x,
y, z) представим в виде:
от точки центра масс до любого поста контроля
АСКРО значительно больше характерного размера облака, объемную активность q(x,
y, z) представим в виде:
![]() , (2)
, (2)
где d(х) - дельта функция. Проводя в уравнении (1), интегрирование по объему с q(x, y, z) вида выражения (2), получаем:
 , (3)
, (3)
где Ri,j,k=Ri; i=1,2,3…Nд,; Nд -
достаточное число детекторов фотонного излучения системы АСКРО. Уравнение (3)
относительно функции j(Е) представляет собой уравнение Фредгольма
первого рода и относится к классу некорректных задач при заданной погрешности DD измерения датчиков
фотонного излучения. Нетривиальное решение этого уравнения возможно, если ![]() . Уравнение
решают заменой j(Е)
групповым спектром, аппроксимацией интеграла конечной суммой и, таким образом,
при различных i задачу сводят к системе линейных алгебраических
уравнений, т.е. решают систему вида:
. Уравнение
решают заменой j(Е)
групповым спектром, аппроксимацией интеграла конечной суммой и, таким образом,
при различных i задачу сводят к системе линейных алгебраических
уравнений, т.е. решают систему вида:
![]() , (4)
, (4)
где ![]() - матрица Nд´M(Nд³M) с матричным элементом ai,j:
- матрица Nд´M(Nд³M) с матричным элементом ai,j:
![]() ;
;
![]() - вектор искомого решения с компонентами jj, j = 1, 2,
3, ... m;
- вектор искомого решения с компонентами jj, j = 1, 2,
3, ... m; ![]() - заданный вектор результатов измерений с
компонентами
- заданный вектор результатов измерений с
компонентами ![]() .
.
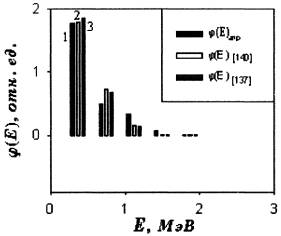
Рис. 1. Гистограммы спектров фотонного излучения: 1 - исходный j(E)апр (Еср=0,567 МэВ), 2 - восстановленный с использованием метода Y. Su (Еср=0,526 МэВ), 3 - восстановленный с использованием метода регуляризации Тихонова А. Н (Еср=0,512 МэВ)
Из
имеющихся методов решения подобных систем уравнений наибольшее применение
получили методы регуляризации [2,
3]
и итеративной регуляризации [4],
в которых искомое решение находят, учитывая погрешность как правой части
уравнения (4), так и оператора ![]() , если она
есть (в данной задаче эта погрешность может быть обусловлена фактором
накопления). Вместе с тем, для задач спектрометрии ионизирующего излучения
разработаны и специальные методы, особенностью которых является жесткое
требование положительности
решения jj³0, j = 1, 2, 3, _ m и отсутствие погрешности в
операторе
, если она
есть (в данной задаче эта погрешность может быть обусловлена фактором
накопления). Вместе с тем, для задач спектрометрии ионизирующего излучения
разработаны и специальные методы, особенностью которых является жесткое
требование положительности
решения jj³0, j = 1, 2, 3, _ m и отсутствие погрешности в
операторе ![]() [5-7].
Для проверки методов расчета jj использует так называемый метод
"бумажного эксперимента": задают исходный спектр jапр(Е), затем по уравнению (3) находят значения D(Ri), которые искажают в пределах погрешности
реальных показаний датчиков (15¸25 %), после чего решают обратную задачу
определения jj.
Из представленных на рис. 1 результатов решения уравнения (4) следует, что
исходный и восстановленный спектры удовлетворительно согласуются, а в табл. 1
вместе с указанными спектрами приведено решение системы линейных алгебраических
уравнений, полученное тривиальным обращением матрицы (неудовлетворительное
решение):
[5-7].
Для проверки методов расчета jj использует так называемый метод
"бумажного эксперимента": задают исходный спектр jапр(Е), затем по уравнению (3) находят значения D(Ri), которые искажают в пределах погрешности
реальных показаний датчиков (15¸25 %), после чего решают обратную задачу
определения jj.
Из представленных на рис. 1 результатов решения уравнения (4) следует, что
исходный и восстановленный спектры удовлетворительно согласуются, а в табл. 1
вместе с указанными спектрами приведено решение системы линейных алгебраических
уравнений, полученное тривиальным обращением матрицы (неудовлетворительное
решение): ![]() , где
, где ![]() - матрица сопряженная
- матрица сопряженная ![]() ,
, ![]() - обратная матрица размером
- обратная матрица размером ![]() ;
; ![]() - вектор.
- вектор.
Таблица 1
Сравнение исходного jапр и восстановленных спектров
|
Индекс j |
Энергия Ej , МэВ |
Cпeктр фи(Ej) |
|||
|
Априорный |
Вычисленный методом |
||||
|
Y.Su |
Тихонова А.Н. |
обр. матр. |
|||
|
1 |
0,37 |
1,768 |
1,784 |
1,851 |
-0,088 |
|
2 |
0,748 |
0,503 |
0,731 |
0,671 |
0,0 |
|
3 |
1,1216 |
0,328 |
0,149 |
0,137 |
-0,802 |
|
4 |
1,496 |
7,36E-2 |
1,56E-2 |
1,45E-2 |
-1,1E-3 |
|
5 |
1,87 |
9,6 E-4 |
2,28E-4 |
2,13E-4 |
2,8434 |
При решении некорректных задач
обычно рассматриваются два случая. В первом задается погрешность в правой части
(векторе ![]() ) и во
втором - погрешность задается правой части и ядре уравнения (3). В
представленном документе ограничиваются первым случаем. Вместе с тем, и в том и
в другом случаях в работе [3]
разработан устойчивый метод решения задачи. Однако для рассматриваемой задачи
могут быть использованы и другие методы: метод N. Sconfield [5], Y. Su [6],
H. Fabian [7].
Эти методы отличаются от метода работы [2]
тем, что они требуют строгой положительности решения, что полностью отвечает
рассматриваемой задаче. Между собой эти методы отличаются определенным
алгоритмом, суть которого сводится к поправке диагональных элементов матрицы.
Последнее определяет скорость сходимости задач, которые решают, используя
итерационные процедуры. Ниже приведены алгоритмы указанных методов, реализация
которых осуществляется пошагово, при этом вектору
) и во
втором - погрешность задается правой части и ядре уравнения (3). В
представленном документе ограничиваются первым случаем. Вместе с тем, и в том и
в другом случаях в работе [3]
разработан устойчивый метод решения задачи. Однако для рассматриваемой задачи
могут быть использованы и другие методы: метод N. Sconfield [5], Y. Su [6],
H. Fabian [7].
Эти методы отличаются от метода работы [2]
тем, что они требуют строгой положительности решения, что полностью отвечает
рассматриваемой задаче. Между собой эти методы отличаются определенным
алгоритмом, суть которого сводится к поправке диагональных элементов матрицы.
Последнее определяет скорость сходимости задач, которые решают, используя
итерационные процедуры. Ниже приведены алгоритмы указанных методов, реализация
которых осуществляется пошагово, при этом вектору ![]() в уравнении (4) соответствует вектор
в уравнении (4) соответствует вектор ![]() в методах I и II, а вектору правой части
в методах I и II, а вектору правой части ![]() соответствует вектор
соответствует вектор ![]() :
:

В работе [7] исходное уравнение имеет аналогичный вид:
 , i =
1, 2, _ m, (5)
, i =
1, 2, _ m, (5)
где Qi,j - элемент
матрицы, соответствующей матричному элементу ai,j матрицы ![]() в уравнении (4); искомый вектор
в уравнении (4); искомый вектор ![]() - вектору
- вектору ![]() ; вектор
правой части
; вектор
правой части ![]() - вектору
- вектору ![]() . Искомый
вектор
. Искомый
вектор ![]() в этой работе находят из уравнения:
в этой работе находят из уравнения:
![]() , (6)
, (6)
в котором
нулевое приближение искомого вектора ![]() находят с помощью единичной диагональной
матрицы d(0)
из уравнения:
находят с помощью единичной диагональной
матрицы d(0)
из уравнения:
![]() . (7)
. (7)
Это
приближение в общем случае не удовлетворяет уравнению (5), но дает возможность
оценить нулевое приближение вектора ![]() :
:
![]() , (8)
, (8)
что
позволяет получить поправочные диагональные элементы матрицы ![]() :
:
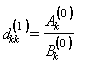 , k =
1, 2, ... m. (9)
, k =
1, 2, ... m. (9)
Таким
образом, полученные оценки матричных элементов диагональной матрицы ![]() позволяют предложить следующий алгоритм
оценки искомого вектора
позволяют предложить следующий алгоритм
оценки искомого вектора ![]() .
.

Если в п. 3 достигается условие сходимости, то решение считается найденным. В ряде случаев целесообразно задавать не погрешность, а число итераций, после чего решение считается найденным. Из рис. 1 следует, что значение средней энергии восстановленных спектров меньше исходного. Последнее нетрудно понять, если учесть, что средняя энергия представленных распределений также представляет собой интегральную величину:
 . Поэтому
наличие погрешности в спектральных распределениях, возникающих при задании
погрешности измерения датчиков, подтверждает справедливость формулы,
описывающей оценку средней величины аргумента случайной функции при заданной ее
относительной погрешности d, которая для средней энергии <Etot> будет
иметь вид: < Etot
> = <Ecp> (1-d).
. Поэтому
наличие погрешности в спектральных распределениях, возникающих при задании
погрешности измерения датчиков, подтверждает справедливость формулы,
описывающей оценку средней величины аргумента случайной функции при заданной ее
относительной погрешности d, которая для средней энергии <Etot> будет
иметь вид: < Etot
> = <Ecp> (1-d).
Следует также отметить, что найденная таким образом средняя энергия фотонного излучения от объемного источника, образовавшегося в результате радиационной аварии на ОИАЭ, по показаниям датчиков системы АСКРО не будет соответствовать какому-либо определенному радионуклиду, но, тем не менее, даст возможность провести оценки радиоактивного загрязнения окружающей среды и дозовых нагрузок на персонал и население.

Рис. 2. Возможное размещение датчиков фотонного излучения в СЗЗ по спирали Архимеда (на пересечении кривой с лучами) и многолучевой звездой в вершинах и основаниях лучей [8]
Таким образом, алгоритм определения спектрального состава фотонного излучения радиоактивной примеси и его средней энергии сводится к следующему:
1. Определению эффективной высоты подъема радиоактивного облака, при использовании показаний технологических датчиков, измеряющих в резервуаре температуру и давление среды.
2. Определению показаний детекторов фотонного излучения системы АСКРО, расположенных на промплощадке и в СЗЗ.
3. Заданию координат датчиков АСКРО и координаты источника с учетом его эффективной высоты.
4.
Вычислению расстояния ![]() от источника до
каждого из детекторов.
от источника до
каждого из детекторов.
5. Определению спектрального состава фотонного излучения радиоактивной примеси, с помощью одного из методов, описанных выше [5], [6], [7].
6. Определению средней энергии фотонного излучения.

Рис. 3. Определение приращения радиуса-вектора Ri и его последующего значения по предыдущему. НI - высота источника; ri - расстояние на подстилающей поверхности от основания источника до детектора фотонного излучения АСКРО
Условие
![]() , i =
1, 2, 3 _ Nд накладывает определенные требования к
размещению детекторов фотонного излучения АСКРО, которые сводятся к исключению
осевой и центральной симметрии при их размещении, поскольку в противном случае
число уравнений вида (3) или (4), отличающихся правой частью, уменьшится в 2
или 4 раза (при осевой симметрии) или приведет к полному вырождению системы
линейных алгебраических уравнений (при размещении датчиков по периметру СЗЗ,
т.е. при центральной симметрии). Кроме того, как уже отмечалось, размещение
датчиков по периметру зоны надежно регистрирует факел выброса или
распространение облака при любом направлении ветра. Учет этих двух
противоречивых требований приводит к тому, что Ri датчиков фотонного излучения должно
возрастать с увеличением азимутального угла, отсчитываемого от какого-либо
направления (например, как в спирали Архимеда). Графики таких кривых приведены
на рис. 2 и представляют собой либо гладкую кривую, для которой Ri, является функцией угла; Ri=R0qi, qi=iDq; I=1, 2, …Nд; Dq=2p/Nд, либо многолучевую звезду. Согласно работе [8],
каждый из датчиков Ni,
где i=1, 2, …Nд;, установлен на расстоянии радиуса-вектора Ri от источника радиоактивных выбросов (на
расстоянии ri
от основания источника), отличном от соответствующих расстояний всех остальных g - датчиков на величину DRi (Dri на подстилающей поверхности) - рис. 3,
причем для Ri£1000 м DRi находят из выражения:
, i =
1, 2, 3 _ Nд накладывает определенные требования к
размещению детекторов фотонного излучения АСКРО, которые сводятся к исключению
осевой и центральной симметрии при их размещении, поскольку в противном случае
число уравнений вида (3) или (4), отличающихся правой частью, уменьшится в 2
или 4 раза (при осевой симметрии) или приведет к полному вырождению системы
линейных алгебраических уравнений (при размещении датчиков по периметру СЗЗ,
т.е. при центральной симметрии). Кроме того, как уже отмечалось, размещение
датчиков по периметру зоны надежно регистрирует факел выброса или
распространение облака при любом направлении ветра. Учет этих двух
противоречивых требований приводит к тому, что Ri датчиков фотонного излучения должно
возрастать с увеличением азимутального угла, отсчитываемого от какого-либо
направления (например, как в спирали Архимеда). Графики таких кривых приведены
на рис. 2 и представляют собой либо гладкую кривую, для которой Ri, является функцией угла; Ri=R0qi, qi=iDq; I=1, 2, …Nд; Dq=2p/Nд, либо многолучевую звезду. Согласно работе [8],
каждый из датчиков Ni,
где i=1, 2, …Nд;, установлен на расстоянии радиуса-вектора Ri от источника радиоактивных выбросов (на
расстоянии ri
от основания источника), отличном от соответствующих расстояний всех остальных g - датчиков на величину DRi (Dri на подстилающей поверхности) - рис. 3,
причем для Ri£1000 м DRi находят из выражения:
![]() , (10)
, (10)
а для Ri£1000 м DRi³W,
где
![]() ; (11)
; (11)

Рис. 4. Определение зависимости DRi как функции радиуса-вектора Ri(DRi=f(Ri))
dD - максимальная относительная погрешность измерения мощности дозы датчиком фотонного излучения; m=m(Eср) - линейный коэффициент ослабления фотонного излучения радиоактивной примеси в воздухе, м-1; Eср - средняя энергия фотонного излучения радиоактивной примеси МэВ. Вывод формул (10), (11) основан на следующих соображениях. Упомянутые выше два противоречивых требований по размещению датчиков АСКРО могут быть учтены, если расстояние от источника выбросов до любого из датчиков контроля Ri будет отличаться от соответствующих расстояний всех остальных датчиков на величину, большую или равную расстоянию между двумя точками на местности, в которых относительная разность мощностей доз от контролируемого источника, по крайней мере, больше или равна величине удвоенного значения максимальной относительной погрешности измерения мощности дозы с помощью используемых датчиков. Эти соображения записываются выражением:
![]() , (12)
, (12)
где D(R+DR), D(R) - значения мощностей доз в точках
(R+DR), (R)
соответственно и ![]() .
.
Поскольку
в бесконечной среде мощность дозы описывается выражением: ![]() , то в
соответствии с формулой (12) получают:
, то в
соответствии с формулой (12) получают:
![]() . (13)
. (13)
Полагая
в последнем B(E,R+DR)»B(E,R), при выполнении неравенства (DR/R)2<<1 получают выражение
(10), а при выполнении неравенства DR/R<<1 - выражение
(11). Практически зависимость DRi=f(Ri), определяемую формулой (10), находят из
графика, который строят согласно выражению (10), используя в качестве аргумента заданные значения Ri. Для Ri>1000 м, R0 находят из условия DRi=Ri+1-Ri=W, что дает R0=NдW/2 и при dD = 30 % и Ecp=1 МэВ, R0=444 м, W = 111 м. При заданном R0 величину r0 определяют из условия: ![]() . При Ri£1000 м минимальное значение Ri выбирают равным
. При Ri£1000 м минимальное значение Ri выбирают равным ![]() , где в качестве высоты источника HI, принимают высоту венттрубы АС, а
последующие значения Ri+1,
Ri+2 находят, используя формулу (10) или
кривую рис. 4 для определения DRi и соотношение: Ri+1=Ri+DRi. При найденных Ri, DRi, расстояния ri на плоскости (подстилающей поверхности)
от основания источника до датчика, при заданной величине HI, для больших и малых Ri, находят, принимая rmin=r1=HI,
из выражений:
, где в качестве высоты источника HI, принимают высоту венттрубы АС, а
последующие значения Ri+1,
Ri+2 находят, используя формулу (10) или
кривую рис. 4 для определения DRi и соотношение: Ri+1=Ri+DRi. При найденных Ri, DRi, расстояния ri на плоскости (подстилающей поверхности)
от основания источника до датчика, при заданной величине HI, для больших и малых Ri, находят, принимая rmin=r1=HI,
из выражений:
 (14)
(14)
Таким образом, предложенный метод расстановки детекторов фотонного излучения АСКРО, с учетом их необходимого и достаточного количества и равномерности азимутального распределения вокруг АС, удовлетворяет экономическим, экологическим и физическим принципам, которые дают основание говорить, что расстановка постов контроля, выполненная указанным методом, действительно является оптимальной.
Список литературы к Приложению № 21
1. Машкович В.П., Кудрявцева А.В. Защита от ионизирующих излучений. Справочник. М.: Энергоатомиздат, 1995, 496 с.
2. Тихонов А.Н. О решении некорректно поставленных задач и метод регуляризации. ДАН СССР, 1963, т. 191, № 3, с. 501-509.
3. Тихонов А.Н. Об устойчивости обратных задач. ДАН СССР, 1943, Т. 39, № 5, с. 195-198.
4. Фридман В.М. Метод последовательных приближений для интегральных уравнений Фредгольма I-го рода. Успехи математических наук, 1956, Т. 11, № 1, с. 233-234.
5. Sconfield N. Proc. Symp. NAS-NS 3017, 1962, p. 108.
6. Su Y. Study of scintillatio№ spectrometry unfolding methods. nucl. Instr. Meth., 1967, v. 54, p. 109-115.
7. Fabian H.U., Nemsman U. Determination of the energy spectrum of a gamma-ray flash. - Atomkernenergie, 1970, BD 16, S. 143-145.
8. Елохин А.П., Pay Д.Ф. Система контроля радиационной обстановки в зонах размещения объектов атомной промышленности. Патент РФ № 2042157, бюллетень № 23 от 20.08.95.
Приложение № 22
Метод уточнения величины мощности выброса
При постановке задачи в выражение, описывающее источник выброса радиоактивной примеси в уравнении (14) Приложения № 4, входит множителем мощность выброса Рв. Если рассматриваемая примесь является радиоактивной, что и будем предполагать в дальнейшем, то мощность выброса будет определяться произведением расхода G [м3/с] на объемную активность примеси Q [Кюри/м3] (Рв=GQ). Поэтому для определения мощности выброса необходимо измерять две величины: расход G и объемную активность Q. Разработки датчиков, непосредственно измеряющих мощность выброса, в настоящее время отсутствуют. Величину расхода, в основном, определяют, исходя из полной мощности вентиляционных установок, имеющих вывод в венттрубу. Объемная активность не может определяться в динамическом режиме, поэтому величина мощности выброса известна со значительной погрешностью. Вместе с тем, с уточнением мощности выброса корректируется как объемная активность воздушного бассейна, так и масштабы радиоактивного загрязнения окружающей среды в целом.
Воспользуемся
тем, что уравнение (14) Приложения № 4
является линейными и мощность выброса в решение входит линейно, поэтому,
рассчитывая некоторую интегральную величину, в которую мощность выброса входит
как множитель (например, мощность дозы от факела радиоактивных выбросов), и
измеряя эту величину, например, датчиками АСКРО, полагая при этом, что их
количество должно быть достаточным в СЗЗ [1,
2],
численное значение величины мощности выброса найдется как отношение измеренной
величины мощности дозы к расчетной (при ![]() - единичной мощности выброса, т.е., где
- единичной мощности выброса, т.е., где ![]() - измеренное значение мощности дозы,
- измеренное значение мощности дозы, ![]() - расчетное значение при единичной мощности).
В общем случае алгоритм определения численного значения величины Рв
выглядит следующим образом.
- расчетное значение при единичной мощности).
В общем случае алгоритм определения численного значения величины Рв
выглядит следующим образом.
1. Выбирают датчик, ближайший к оси следа выброса на подстилающей поверхности.
2.
Регистрируют показания этого датчика в различные моменты времени ![]() , где
i = 1, 2, 3, _, L, учитывая
нестационарность процесса переноса радиоактивного облака при его движении вдоль
оси.
, где
i = 1, 2, 3, _, L, учитывая
нестационарность процесса переноса радиоактивного облака при его движении вдоль
оси.
3. Находят момент времени t*, в котором показание будет максимальным.
4.
Вычисляют в тот же момент времени в точке выбранного датчика мощность дозы ![]() при Pв=1, т.е. находят:
при Pв=1, т.е. находят:
 ,
,
в
которой ![]() рассчитано по уравнениям (14) и (1)
Приложений № 20,
21
при Pв=1.
рассчитано по уравнениям (14) и (1)
Приложений № 20,
21
при Pв=1.
5.
Так как ![]() , то
измеренная величина
, то
измеренная величина ![]() и рассчитанная при Pв=1 определяются
соотношением:
и рассчитанная при Pв=1 определяются
соотношением: ![]() , что
и позволяет найти искомое значение
, что
и позволяет найти искомое значение ![]() .
.
6.
Если в области распространения следа радиоактивного облака окажется несколько
датчиков i = 1,
2, ..., N' то,
осуществляя подобную процедуру для каждого i-го датчика, абсолютное численное
значение Pв
находят как среднеквадратичное  .
Такая оценка позволит избежать влияния нестабильной работы какого-нибудь одного
из датчиков на величину Pв.
.
Такая оценка позволит избежать влияния нестабильной работы какого-нибудь одного
из датчиков на величину Pв.
Для стационарного выброса, измеряя величину мощности дозы внешнего облучения датчиками АСКРО, полагая при этом, что их количество удовлетворяет критерию достаточности, численное значение мощности выброса найдется как отношение величин мощностей доз измеренной и расчетной (при единичной мощности выброса) по формуле:
![]() ,
,
где ![]() - измеренное значение мощности дозы,
- измеренное значение мощности дозы, ![]() - расчетное значение при единичной мощности.
- расчетное значение при единичной мощности.
После умножения на Pв всех искомых функционалов, вычисленных с qед(x, y, z, t), получают распределения в абсолютных единицах.
При
этом следует учитывать, что с уменьшением измеряемой мощности дозы ![]() увеличивается относительный вклад фонового
значения мощности дозы, и, таким образом, растет погрешность мощности выброса.
Чтобы убедиться в этом рассмотрим оценку величины мощности выброса при наличии
естественного или техногенного фона фотонного излучения.
увеличивается относительный вклад фонового
значения мощности дозы, и, таким образом, растет погрешность мощности выброса.
Чтобы убедиться в этом рассмотрим оценку величины мощности выброса при наличии
естественного или техногенного фона фотонного излучения.
Пусть
величина ![]() представляет собой фоновую мощность дозы,
создаваемую фотонным излучением естественного или техногенного происхождения, а
измерение мощности дозы в условиях аварийного выброса осуществляется в двух
точках на расстояниях Y1
и Y2,
(Y1<
Y2),
отстоящих от оси выброса X, представляющих соответственно значения
представляет собой фоновую мощность дозы,
создаваемую фотонным излучением естественного или техногенного происхождения, а
измерение мощности дозы в условиях аварийного выброса осуществляется в двух
точках на расстояниях Y1
и Y2,
(Y1<
Y2),
отстоящих от оси выброса X, представляющих соответственно значения ![]() и
и ![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству ![]() (рис. 1).
(рис. 1).

Рис. 1. Оценка величины мощности выброса радиоактивной примеси в атмосферу с учетом фоновых значений мощности дозы естественного или техногенного происхождения
Введем
значение веса di,
представляющего собой относительный вклад разности измеренного значения
мощности дозы за вычетом фонового значения к ее абсолютной величине  . Очевидно,
что при выполнении указанных неравенств d1>d2 и d2~0, если
. Очевидно,
что при выполнении указанных неравенств d1>d2 и d2~0, если ![]() . При
определенных нами условиях величины d1 и d2 будут представлять собой следующее:
. При
определенных нами условиях величины d1 и d2 будут представлять собой следующее: 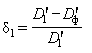 ,
,  , а
численные значения мощности выброса, измеряемого при нормировке на тот или
другой детектор, с учетом весов будут определяться соответственно выражениями:
, а
численные значения мощности выброса, измеряемого при нормировке на тот или
другой детектор, с учетом весов будут определяться соответственно выражениями:
![]() ,
, ![]() и
и ![]() .
.
Таким
образом, с учетом фоновых значений, общее выражение для численного значения
мощности выброса определится выражением: 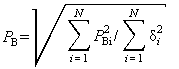 , где
, где ![]() и
и ![]() . После
умножения всех искомых функционалов на Pв, вычисленных с qед(x, y, z, t), получим распределения в абсолютных
единицах.
. После
умножения всех искомых функционалов на Pв, вычисленных с qед(x, y, z, t), получим распределения в абсолютных
единицах.
Список литературы к Приложению № 22
1. Корн Г, Корн Т. Справочник по математике (для научных работников и инженеров). М.: Наука, 1974, с. 48.
2. Елохин А.П., Соловей А.Ф. Оценка и прогнозирование масштабов радиоактивного загрязнения окружающей среды при выбросах АЭС. Атомная энергия, т. 77, вып. 2, 1994, с. 145-152.
Приложение № 23
Метод выбора наиболее оптимального датчика для нормировки
Если детекторы фотонного излучения дозиметрического контроля (датчики АСКРО), расположенные в C33, зафиксировать в полярной системе координат z=z( Ri, jI), где Ri - радиус i-го детектора, ji - азимутальный угол, под которым детектор расположен относительно начала отсчета (с севера на юг по часовой стрелке), то при задании направления выброса (биссектрисы раствора факела), задаваемого углом jb, один из детекторов фотонного излучения будет расположен наиболее близко к оси выброса (рис. 1). Очевидно, что мощность дозы, регистрируемая этим датчиком АСКРО, будет выше, чем у других. Поэтому и мощность выброса следует определять по этому датчику.
Алгоритм определения датчика ближайшего к оси выброса выглядит следующим образом.
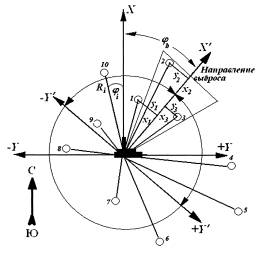
Рис. 1 Геометрия определения координат и номера датчика, ближайшего к оси выброса радиоактивной примеси 1 -10 - детекторы фотонного излучения постов контроля АСКРО, (X,Y) -жесткая система координат, (Х',Y) -локальная система координат
1. При заданном направлении выброса, датчик ближайший к оси выброса, находят, выбирая минимальное значение тангенса угла датчиков ACKPO, расположенных в растворе (- 90, + 90) относительно направления выброса (рис. 1).
2. Если тангенсы углов, под которыми расположены несколько датчиков относительно направления выброса, будут равны, то ближайшим к оси выбирается детектор, имеющий меньший радиус Ri. Аналогично поступают, если детекторы лежат на одной прямой (на одном луче).
3. Значение мощности дозы каждого датчика в СЗЗ фиксируется в ЭВМ и хранится в таблице под своим номером "i". Для датчика, выбранного ближайшим к оси выброса, определяют декартовы координаты (xi,yi) с осью "X¢" вдоль направления выброса и его номер "i", по которому затем находят значение мощности дозы, регистрируемое этим датчиком.

Приложение № 24
Термины и определения
1. Мощность выброса радиоактивной примеси, [Бк/с] - величина, равная произведению секундного расхода G [м3/с] на объемную активность Аv [Бк/м3].
2. Орография подстилающей поверхности - особенности региона, учитывающие своеобразность рельефа подстилающей поверхности и ее шероховатость.
3. Пограничный слой атмосферы - прилегающий к земной поверхности слой атмосферы высотой в среднем около 1000 м, свойства которого, в основном, определяются динамичными и тепловыми воздействиями земной поверхности.
4. Приземный слой атмосферы - часть пограничного слоя атмосферы; нижний, прилегающий к земной поверхности слой тропосферы толщиной 30-50 м (иногда до 250 м), свойства которого в значительной степени определяются близостью подстилающей поверхности; в этом слое атмосферы скорость ветра, температура и влажность воздуха особенно быстро меняются с высотой, а также обычно возникают приземные инверсии температуры, туманы, заморозки, скапливаются загрязнения.
5. Состояние устойчивости пограничного слоя атмосферы - состояние пограничного слоя атмосферы, характеризуемое относительно устойчивыми во времени полями метеорологических элементов (температурой, скоростью ветра, его направлением, влажностью и т.д.).
6. Шероховатость подстилающей поверхности - неровности подстилающей поверхности, в частности, городские строения, растительный покров, снежный покров и другие факторы, оказывающие значительное влияние на характер распространения воздушного потока. Влияние таких неровностей учитывается с помощью изменения параметра шероховатости z0.